Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Kẻ \(HM \bot AB\) và \(HN \bot AC\). Chứng minh \(AM.AB = AN.AC\)
Giải bởi Vietjack
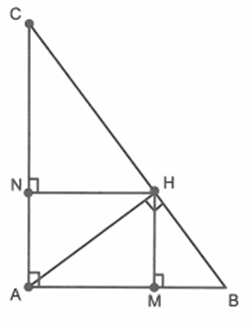
Xét \(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {MAH}\) chung; \(\widehat {AMH} = \widehat {AHB} = 90^\circ \)
\( \Rightarrow \Delta AHM\~\Delta AHB\) (g.g) \( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AM}}{{AH}} \Rightarrow A{H^2} = AM.AB\) (1)
Xét \(\Delta AHN\) và \(\Delta ABH\) có: \(\widehat {NAH}\) chung; \(\widehat {ANH} = \widehat {AHC} = 90^\circ \)
\( \Rightarrow \Delta AHN\~\Delta ACH\)\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{AN}}{{AH}} \Rightarrow A{H^2} = AN.AC\] (2)
Từ (1), (2) suy ra: \[AM.AB = AN.AC\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\] và \[\Delta CDM\] cânCho tam giác ABC có \[AB = 18cm,\,AC = 24cm,\,BC = 30cm\]. Gọi M là trung điểm của BC. Qua M kẻ đường vuông góc với BC cắt AB, AC lần lượt ở D, E.
Chứng minh rằng: \[\Delta ABC\sim\Delta MDC\]
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Tính BD và CD
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích \[\Delta ABC\] là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích \[\Delta MND\].
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[A{D^2} = AB.AC - BD.CD\]
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta FHE\sim\Delta BHC\]
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[AE.AC = AF.AB\]
Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\].
Chứng minh \[\Delta DAB\sim\Delta CBD\].
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta AFE\sim\Delta ACB\]
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[\Delta ADB\~\Delta ACI;\,\,\Delta ADB\sim\Delta CDI\]
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho \[\widehat {DME} = \widehat B\]
Chứng minh rằng \[\Delta MDE\sim\Delta DBM\]
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\sim\Delta MDC\]
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[MA.MC = MD.ME\]
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Tính AC
Cho tam giác ABC vuông tại A, đường cao AH. Biết \[AB = 4cm,\,AC = 3cm\].
Tính độ dài CH.
