Trắc nghiệm Chuyên đề toán 9 Chuyên đề 1: Tam giác đồng dạng, Định lí Talet có đáp án
Chủ đề 2: Tam giác đồng dạng có đáp án
-
785 lượt thi
-
48 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có \[AB = 6cm,\,AC = 9cm,\,BC = 12cm\] và \[\Delta MNP\] có \[MN = 24cm,\,NP = 18cm,\,MP = 12cm\].
Chứng minh \[\Delta ABC \sim \Delta MNP\].
 Xem đáp án
Xem đáp án
Ta có: \[\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MN}} = \frac{1}{2}\] nên \[\Delta ABC \sim \Delta PMN\] (c.c.c).
Câu 2:
Cho tam giác ABC có \[AB = 6cm,\,AC = 9cm,\,BC = 12cm\] và \[\Delta MNP\] có \[MN = 24cm,\,NP = 18cm,\,MP = 12cm\].
Tính tỉ số diện tích của hai tam giác trên.
 Xem đáp án
Xem đáp án
Do \[\Delta ABC \sim \Delta PMN\] nên \[\frac{{{S_{\Delta ABC}}}}{{{S_{\Delta MNP}}}} = {\left( {\frac{{AB}}{{MP}}} \right)^2} = \frac{1}{4}\].
Câu 3:
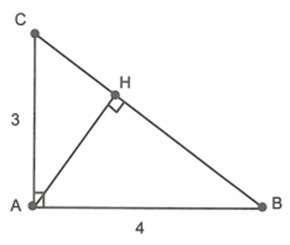
Cho tam giác ABC vuông tại A, đường cao AH. Biết \[AB = 4cm,\,AC = 3cm\].
Chứng minh \[\Delta HAC\sim\Delta ABC\].
 Xem đáp án
Xem đáp án
Xét \[\Delta HAC\] và \[\Delta ABC\] có: \[\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\] chung nên \[\Delta HAC\sim\Delta ABC\] (g.g).
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Biết \[AB = 4cm,\,AC = 3cm\].
Tính độ dài CH.
 Xem đáp án
Xem đáp án
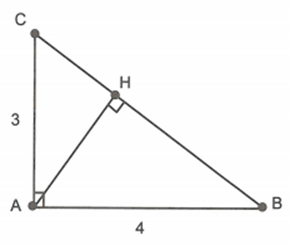
Áp dụng định lí Pitago cho tam giác vuông ABC ta dễ dàng tính được \[BC = 5cm\].
Do \[\Delta HAC\~\Delta ABC\] nên
\[\frac{{CH}}{{CA}} = \frac{{AC}}{{BC}} \Rightarrow \frac{{CH}}{3} = \frac{3}{5} \Rightarrow CH = 1,8cm\]
Câu 5:
Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\].
Chứng minh \[\Delta DAB\sim\Delta CBD\].
 Xem đáp án
Xem đáp án
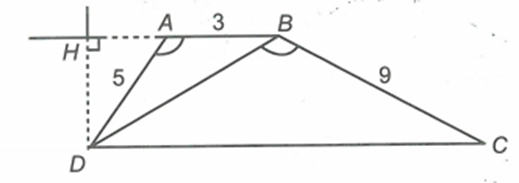
\[AB\parallel CD \Rightarrow \widehat {ABD} = \widehat {BDC}\].
Xét \[\Delta DAB\] và \[\Delta CBD\] có: \[\widehat {DAB} = \widehat {DBC};\,\widehat {ABD} = \widehat {BDC}\] nên \[\Delta DAB\sim\Delta CBD\] (g.g).Câu 6:
Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\]
Từ câu a, tính độ dài DB, DC.
 Xem đáp án
Xem đáp án
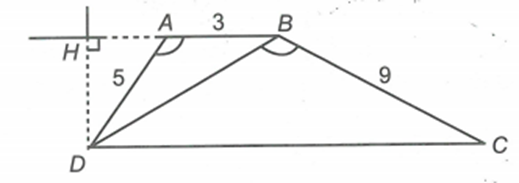
\[\Delta DAB\~\Delta CBD \Rightarrow \frac{{DA}}{{CB}} = \frac{{AB}}{{BD}} = \frac{{DB}}{{CD}} \Rightarrow \frac{5}{9} = \frac{3}{{BD}} = \frac{{BD}}{{CD}} \Rightarrow BD = 5,4cm;\,CD = 9,72cm\].
Câu 7:
Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\]
Tính diện tích hình thang ABCD, biết diện tích tam giác ABD bằng 5cm2
 Xem đáp án
Xem đáp án
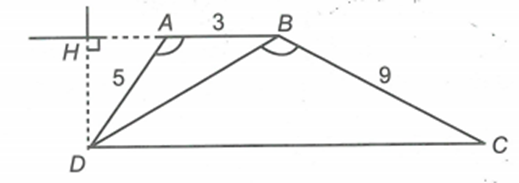
Kẻ DH vuông góc với AB tại H
Theo giả thiết: \[{S_{ABD}} = 5 \Rightarrow \frac{1}{2}DH.AB = 5 \Rightarrow DH = \frac{{10}}{3}cm\].
Từ đó: \[{S_{ABCD}} = \frac{1}{2}DH(AB + CD) = \frac{1}{2}.\frac{{10}}{3}(3 + 9,72) = \frac{{106}}{5}c{m^2}\]
Câu 8:
Cho \[DE\parallel BC\], D là một điểm trên cạnh AB, E là một điểm trên cạnh AC sao cho \[DE\parallel BC\]. Xác định vị trí của điểm D sao cho chu vi tam giác ADE bằng \[\frac{2}{5}\] chu vi tam giác ABC. Tính chu vi của hai tam giác đó, biết tổng 2 chu vi bằng 63cm.
 Xem đáp án
Xem đáp án
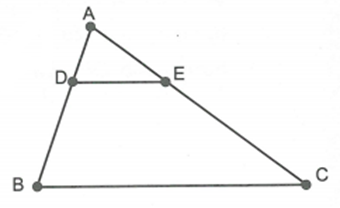
Do \[DE\parallel BC\] nên dễ dàng chứng minh được \[\Delta ADE\~\Delta ABC\] (g.g) với tỉ số đồng dạng \[k = \frac{{AD}}{{AB}}\].
Khi đó \[AD = kAB,\,AE = kAC\] và \[DE = kBC\] nên \[C{V_{\Delta ADE}} = k.C{V_{\Delta ABC}}\] (1).
Theo giả thiết chu vi tam giác ADE bằng \[\frac{2}{5}\] chu vi tam giác ABC suy ra \[k = \frac{2}{5}\].
Vậy \[AD = \frac{2}{5}AB\].
Từ (1) suy ra \[\frac{{C{V_{\Delta ADE}}}}{k} = \frac{{C{V_{\Delta ABC}}}}{1} = \frac{{C{V_{\Delta ADE}} + C{V_{\Delta ABC}}}}{{1 + k}} = \frac{{63}}{{1 + \frac{2}{5}}} = 45\]
\[ \Rightarrow C{V_{\Delta ADE}} = 18cm,\,\,C{V_{\Delta ABC}} = 45cm\]
Câu 9:
Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
Chứng minh \(\Delta DEC \sim \Delta ABC\)
 Xem đáp án
Xem đáp án
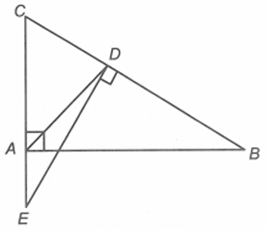
Xét tam giác \(\Delta DEC\) và \(\Delta ABC\) có: \(\widehat C\) chung; \(\widehat {CDE} = \widehat {BAC} = 90^\circ \) nên \(\Delta DEC\~\Delta ABC\) (g.g)
Câu 10:
Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
Chứng minh \(DE = DB\)
 Xem đáp án
Xem đáp án
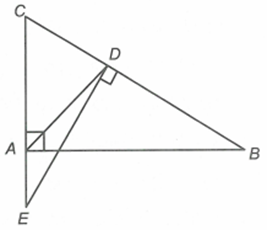
Do \(\Delta DEC\~\Delta ABC\) nên \(\frac{{DE}}{{AB}} = \frac{{CD}}{{AC}}\) (1)
Mặt khác, AD là tia phân giác của \(\widehat {BAC}\) nên theo tính chất đường phân giác ta có: \(\frac{{CD}}{{AC}} = \frac{{BD}}{{AB}}\) (2)
Từ (1), (2) suy ra \(\frac{{DE}}{{AB}} = \frac{{BD}}{{AB}}\) hay \(DE = BD\)
Câu 11:
Cho tam giác \(\Delta ABC\) có \(AB = 9cm,\,\,AC = 6cm\). Điểm D nằm trên cạnh AB sao cho \(AD = 2cm\). Gọi E là trung điểm của AC. Chứng minh \(\Delta AED\sim\Delta ABC\)
 Xem đáp án
Xem đáp án
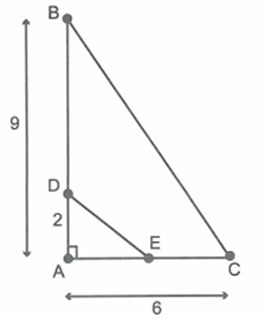
Ta có: \(AE = 3,\,\,AD = 3,\,\,AC = 6,\,\,AB = 9\) suy ra \(\frac{{AD}}{{AC}} = \frac{{AE}}{{AB}} = \frac{1}{3}\)
Xét \(\Delta AED\) và \(\Delta ABC\) có: \(\widehat A\) chung, \(\frac{{AD}}{{AC}} = \frac{{AE}}{{AB}}\)
\( \Rightarrow \)\(\Delta AED\sim\Delta ABC\) (c.g.c).Câu 12:
Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Chứng minh rằng: \(\Delta AHB\sim\Delta CAB\). Từ đó suy ra \(A{B^2} = HB.BC\)
 Xem đáp án
Xem đáp án
xét hai tam giác \(\Delta AHB\) và \(\Delta CAB\) có: \(\widehat {ABH}\) chung, \(\widehat {BHA} = 90^\circ ,\,\,\widehat {BAC} = 90^\circ \)
\( \Rightarrow \Delta AHB\sim\Delta CAB\) (g.g)
Do \(\Delta AHB\~\Delta CAB\) nên \(\frac{{HB}}{{AB}} = \frac{{AB}}{{BC}}\), từ đó suy ra \(A{B^2} = HB.BC\)
Câu 13:
Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
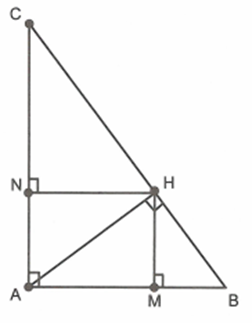
Kẻ \(HM \bot AB\) và \(HN \bot AC\). Chứng minh \(AM.AB = AN.AC\)
 Xem đáp án
Xem đáp án
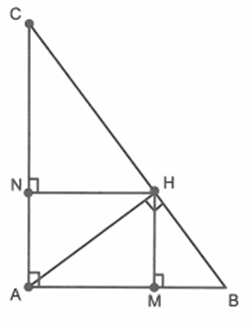
Xét \(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {MAH}\) chung; \(\widehat {AMH} = \widehat {AHB} = 90^\circ \)
\( \Rightarrow \Delta AHM\~\Delta AHB\) (g.g) \( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AM}}{{AH}} \Rightarrow A{H^2} = AM.AB\) (1)
Xét \(\Delta AHN\) và \(\Delta ABH\) có: \(\widehat {NAH}\) chung; \(\widehat {ANH} = \widehat {AHC} = 90^\circ \)
\( \Rightarrow \Delta AHN\~\Delta ACH\)\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{AN}}{{AH}} \Rightarrow A{H^2} = AN.AC\] (2)
Từ (1), (2) suy ra: \[AM.AB = AN.AC\]
Câu 14:
Cho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Chứng minh \(\Delta AMN\sim\Delta ACB\)
 Xem đáp án
Xem đáp án
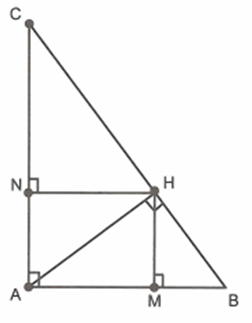
Ta có: \[AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\]
Xét \[\Delta AMN\] và \[\Delta ABC\] có: \[\widehat {MAN}\] chung; \[\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\] nên \(\Delta AMN\sim\Delta ACB\) (c.g.c)
Câu 15:
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho \[\widehat {DME} = \widehat B\]
Chứng minh rằng \[\Delta BDM\sim\Delta CME\]
 Xem đáp án
Xem đáp án
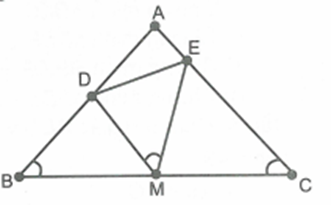
Ta có: \[\widehat {DMC} = \widehat B + \widehat {BDM}\] (góc ngoài tại đỉnh M của tam giác BDM) suy ra \[\widehat B + \widehat {BDM} = \widehat {DME} + \widehat {EMC}\]
Mặt khác, \[\widehat B = \widehat {DME}\] nên ta có \[\widehat {BDM} = \widehat {EMC}\]
Xét \[\Delta BDM\] và \[\Delta CME\] có: \[\widehat {BDM} = \widehat {EMC},\,\,\widehat B = \widehat C\]
Suy ra \[\Delta BDM\sim\Delta CME\] (g.g)
Câu 16:
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho \[\widehat {DME} = \widehat B\]
Chứng minh rằng \[\Delta MDE\sim\Delta DBM\]
 Xem đáp án
Xem đáp án
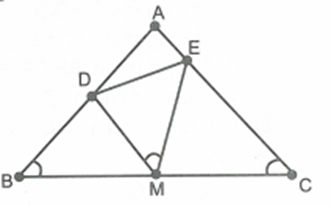
Do \[\Delta BDM\~\Delta CME\] (câu a) nên \[\frac{{BD}}{{CM}} = \frac{{DM}}{{ME}} \Rightarrow \frac{{BD}}{{BM}} = \frac{{DM}}{{ME}} \Rightarrow \frac{{BD}}{{DM}} = \frac{{BM}}{{ME}}\]
Xét \[\Delta MDE\] và \[\Delta DBM\] có: \[\widehat B = \widehat M;\,\,\frac{{BD}}{{DM}} = \frac{{BM}}{{ME}}\] nên \[\Delta MDE\sim\Delta DBM\] (c.g.c)
Câu 17:
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho \[\widehat {DME} = \widehat B\]
Chứng minh rằng không đổi
 Xem đáp án
Xem đáp án
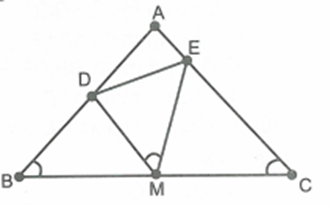
Do \[\Delta BDM\~\Delta CME\] (câu a) nên \[\,\frac{{BD}}{{CM}} = \frac{{BM}}{{CE}} \Rightarrow BD.CE = CM.BM = \frac{{B{C^2}}}{4}\] không đổi
Câu 18:
Cho tam giác ABC có \[AB = 18cm,\,AC = 24cm,\,BC = 30cm\]. Gọi M là trung điểm của BC. Qua M kẻ đường vuông góc với BC cắt AB, AC lần lượt ở D, E.
Chứng minh rằng: \[\Delta ABC\sim\Delta MDC\]
 Xem đáp án
Xem đáp án
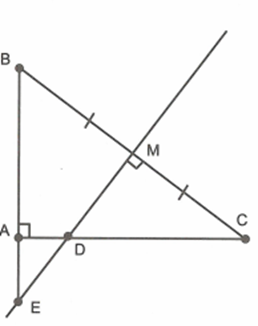
Theo định lí Pitago đảo, chứng minh được \[\Delta ABC\] vuông tại A.
Xét \[\Delta ABC\] và \[\Delta MDC\] có: \[\widehat {BAC} = \widehat {DMC} = 90^\circ ;\,\,\widehat C\] chung
nên \[\Delta ABC\sim\Delta MDC\] (g.g)
Câu 19:
Cho tam giác ABC có \[AB = 18cm,\,AC = 24cm,\,BC = 30cm\]. Gọi M là trung điểm của BC. Qua M kẻ đường vuông góc với BC cắt AB, AC lần lượt ở D, E.
Tính độ dài các cạnh \[\Delta MDC\]
 Xem đáp án
Xem đáp án

Do \[\Delta ABC\~\Delta MDC\] nên
\[\frac{{MD}}{{AB}} = \frac{{MC}}{{AC}} = \frac{{CD}}{{BC}} \Rightarrow \frac{{MD}}{{18}} = \frac{{15}}{{24}} = \frac{{CD}}{{30}}\]
\[ \Rightarrow MD = 11,25cm;\,\,CD = 18,75cm\]
Câu 20:
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích \[\Delta ABC\] là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích \[\Delta MND\].
 Xem đáp án
Xem đáp án
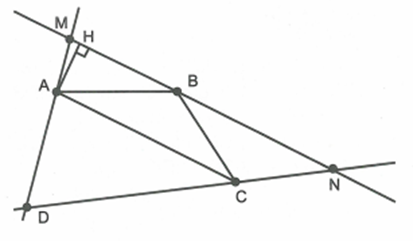
Ta có:
\[{S_{\Delta ADC}} = {S_{ABCD}} - {S_{\Delta ABC}} = 25c{m^2}\]
Dễ dàng chứng minh được \[\Delta DAC\~\Delta DMN\]
Suy ra
\[\frac{{{S_{\Delta ADC}}}}{{{S_{\Delta DMN}}}} = {\left( {\frac{{AC}}{{MN}}} \right)^2} = {k^2}\]
Kẻ \[AH \bot MN\]
Đặt \[{S_{\Delta DMN}} = S,\,\,{S_{\Delta ADC}} = {S_1},\,{S_{ACNM}} = {S_2}\] thì ta có:
\[{S_1} = {k^2}S \Rightarrow S = \frac{{{S_1}}}{{{k^2}}} = \frac{{25}}{{{k^2}}}\]
\[{S_{\Delta ABC}} = \frac{1}{2}AH.AC\]
\[{S_2} = {S_{\Delta AMB}} + {S_{\Delta BCN}} + {S_{\Delta ABC}} = \frac{1}{2}AH.MB + \frac{1}{2}AH.NB + \frac{1}{2}AH.AC\]
\[ = \frac{1}{2}AH(MN + AC) = \frac{1}{2}AH.\left( {\frac{{AC}}{k} + AC} \right) = \frac{{k + 1}}{k}{S_{\Delta ABC}}\]
\[ \Rightarrow {S_2} = \frac{{11(k + 1)}}{k}\]
Mặt khác \[S = {S_1} + {S_2} \Rightarrow \frac{{25}}{{{k^2}}} = 25 + \frac{{11(k + 1)}}{k} \Leftrightarrow 25{k^2} + 11k(k + 1) - 25 = 0 \Leftrightarrow k = \frac{{25}}{{36}}\]
Vậy \[S = 51,84c{m^2}\]
Câu 21:
Cho tam giác ABC có ba góc nhọn, đường cao AH \[(H \in BC)\]. Kẻ tại D, \[HE \bot AC\] tại E.
Chứng minh \[\Delta AHB\sim\Delta ADH,\,\,\Delta AHC\sim\Delta AEH\]
 Xem đáp án
Xem đáp án
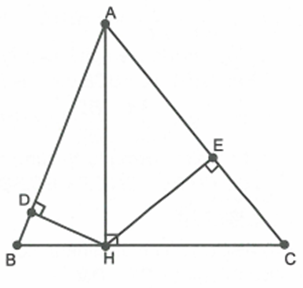
Xét \[\Delta AHB\] và \[\Delta ADH\] có: \[\widehat {BAH}\] chung;
\[\widehat {ADH} = \widehat {AHB} = 90^\circ \] nên \[\Delta AHB\sim\Delta ADH\] (g.g)
Chứng minh tương tự ta cũng có: \[\Delta AHC\sim\Delta AEH\] (g.g)
Câu 22:
Cho tam giác ABC có ba góc nhọn, đường cao AH \[(H \in BC)\]. Kẻ tại D, \[HE \bot AC\] tại E.
Chứng minh \[AE.AC = AD.AB\]
 Xem đáp án
Xem đáp án
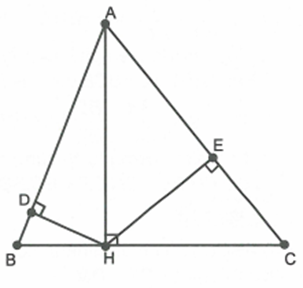
Do \[\Delta AHB\~\Delta ADH\] nên
\[\frac{{AH}}{{AD}} = \frac{{AB}}{{AH}} \Rightarrow AB.AD = A{H^2}\]
Do \[\Delta AHC\~\Delta AEH\] nên \[\frac{{AH}}{{AE}} = \frac{{AC}}{{AH}} \Rightarrow AE.AC = A{H^2}\]
Từ đó suy ra \[AE.AC = AB.AD\]
Câu 23:
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[\Delta ADB\~\Delta ACI;\,\,\Delta ADB\sim\Delta CDI\]
 Xem đáp án
Xem đáp án
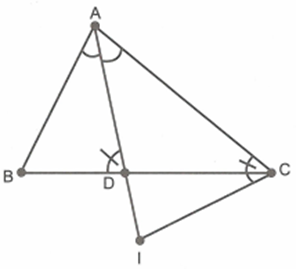
Xét \[\Delta ADB\] và \[\Delta ACI\] có: \[\widehat {BAD} = \widehat {IAC}\] (do AD là phân giác), \[\widehat {ACI} = \widehat {BDA}\] (giả thiết) suy ra \[\Delta ADB\~\Delta ACI\] (g.g)
Do \[\Delta ADB\~\Delta ACI\] nên \[\widehat {ABD} = \widehat {AIC}\]
Xét \[\Delta ADB\] và \[\Delta CDI\] có: \[\widehat {ABD} = \widehat {AIC};\,\,\widehat {ADB} = \widehat {CDI}\] (đối đỉnh) suy ra \[\Delta ADB\sim\Delta CDI\] (g.g)
Câu 24:
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[A{D^2} = AB.AC - BD.CD\]
 Xem đáp án
Xem đáp án
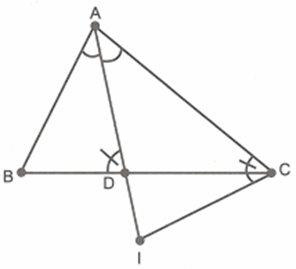
Do \[\Delta ADB\~\Delta ACI\] nên \[\frac{{AD}}{{AC}} = \frac{{AB}}{{AI}} \Rightarrow AB.AC = AD.AI\]
Do \[\Delta ADB\~\Delta CDI\] nên \[\frac{{AD}}{{CD}} = \frac{{DB}}{{DI}} \Rightarrow BD.CD = AD.DI\]
Do đó \[AB.AC - BD.CD = AD.AI - AD.DI = A{D^2}\] (đpcm)
Câu 25:
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[AE.AC = AF.AB\]
 Xem đáp án
Xem đáp án
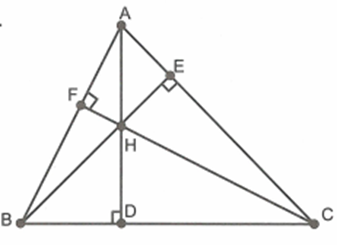
Xét \[\Delta ACF\] và \[\Delta ABE\] có: \[\widehat {BAC}\] chung; \[\widehat {AEB} = \widehat {AFC} = 90^\circ \] nên \[\Delta ACF\~\Delta ABE\] (g.g)
Do đó, ta có: \[\frac{{AC}}{{AB}} = \frac{{AF}}{{AE}}\] hay \[AC.AE = AB.AF\]
Câu 26:
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta AFE\sim\Delta ACB\]
 Xem đáp án
Xem đáp án
Theo câu a) \[\frac{{AC}}{{AB}} = \frac{{AF}}{{AE}} \Rightarrow \frac{{AC}}{{AF}} = \frac{{AB}}{{AE}}\]
Xét \[\Delta AEF\] và \[\Delta ABC\] có: \[\widehat {BAC}\] chung; \[\frac{{AC}}{{AF}} = \frac{{AB}}{{AE}}\] nên \[\Delta AEF\sim\Delta ABC\] (c.g.c)Câu 27:
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta FHE\sim\Delta BHC\]
 Xem đáp án
Xem đáp án
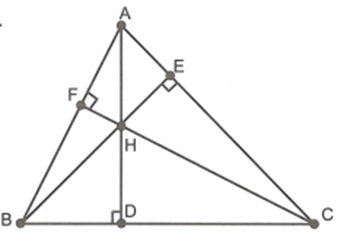
Xét \[\Delta BHF\] và \[\Delta CHE\] có: \[\widehat {BFH} = \widehat {CEH} = 90^\circ ;\,\,\widehat {BHF} = \widehat {CHE}\] (đối đỉnh) nên \[\Delta BHF\~\Delta CHE\] (g.g)
Từ đó suy ra \[\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}} \Rightarrow \frac{{HF}}{{HB}} = \frac{{HE}}{{HC}}\]
Xét \[\Delta HEF\] và \[\Delta HCB\] có: \[\widehat {EHF} = \widehat {BHC}\] (đối đỉnh); \[\frac{{HF}}{{HB}} = \frac{{HE}}{{HC}}\] nên \[\Delta HEF\sim\Delta HCB\] (c.g.c) (đpcm)
Câu 28:
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[HA.HD = HB.HE = HC.HF\]
 Xem đáp án
Xem đáp án
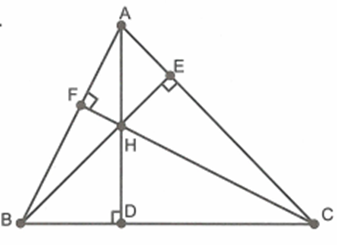
Do \[\frac{{HF}}{{HB}} = \frac{{HE}}{{HC}}\] nên \[HB.HE = HC.HF\]. Chứng minh tương tự ta cũng có: \[HB.HE = HA.HD\]
Từ đó ta được điều phải chứng minh.
Câu 29:
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[B{C^2} = BH.BE + CH.CF\]
 Xem đáp án
Xem đáp án
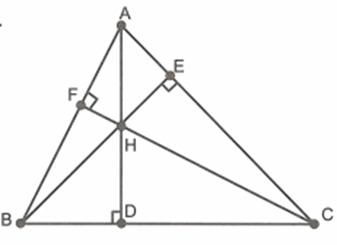
Xét \[\Delta BHD\] và \[\Delta BCE\] có: \[\widehat {CBE}\] chung; \[\widehat {BDH} = \widehat {BEC} = 90^\circ \] nên \[\Delta BHD\~\Delta BCE\] (g.g)
Từ đó suy ra \[\frac{{BH}}{{BC}} = \frac{{BD}}{{BE}}\] hay \[BH.BE = BC.BD\]
Chứng minh tương tự ta cũng có: \[CH.CF = CD.CB\]
Do đó \[BH.BE + CH.CF = BC.BD + CD.BC = BC(CD + CD) = B{C^2}\] (đpcm)
Câu 30:
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\] và \[\Delta CDM\] cân Xem đáp án
Xem đáp án
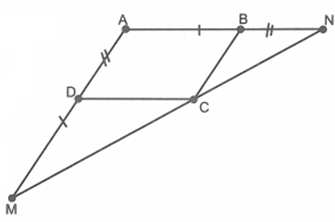
ABCD là hình bình hành nên \[AB = CD\], mà \[AB = DM\] (giả thiết) nên \[CD = CM\]
Do đó tam giác CDM cân tại D
Chứng minh tương tự ta có tam giác CBN cân tại B.
Câu 31:
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\sim\Delta MDC\]
 Xem đáp án
Xem đáp án
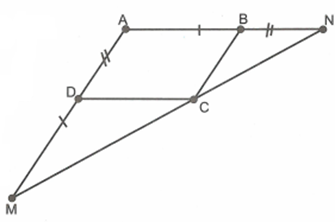
Từ câu a) suy ra \[\frac{{DM}}{{BC}} = \frac{{CD}}{{BN}}\]
Dễ dàng chứng minh được \[\widehat {MDC} = \widehat {CBN}( = \widehat {DAB})\]
Do đó \[\Delta MDC\sim\Delta CBN\] (c.g.c) (đpcm)
Câu 32:
Cho hình thoi ABCD có \[\widehat A = 60^\circ \]. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt đường thẳng AB tại E và cắt đường thẳng AD tại F.
Chứng minh \[\Delta BEC\sim\Delta AEF\]
 Xem đáp án
Xem đáp án
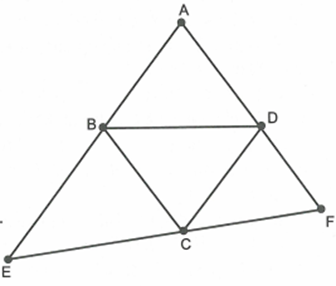
ABCD là hình thoi nên \[BC\parallel AD\]
\[ \Rightarrow \frac{{EB}}{{EA}} = \frac{{EC}}{{EF}}\]
Xét \[\Delta BEC\] và \[\Delta AEF\] có : \[\widehat {BEC}\] chung, \[\frac{{EB}}{{EA}} = \frac{{EC}}{{EF}}\] nên \[\Delta BEC\sim\Delta AEF\] (c.g.c)
Câu 33:
Cho hình thoi ABCD có \[\widehat A = 60^\circ \]. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt đường thẳng AB tại E và cắt đường thẳng AD tại F.
Chứng minh \[\Delta DCF\sim\Delta AEF\]
 Xem đáp án
Xem đáp án
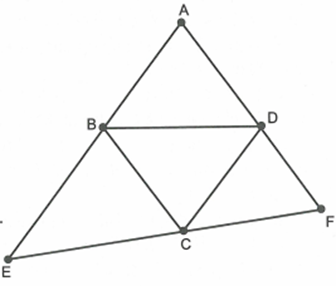
Chứng minh tương tự bài trước
Câu 34:
Cho hình thoi ABCD có \[\widehat A = 60^\circ \]. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt đường thẳng AB tại E và cắt đường thẳng AD tại F.
Chứng minh \[BE.DF = D{B^2}\]
 Xem đáp án
Xem đáp án
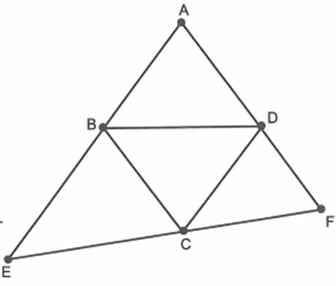
Do \[BE\parallel DC\] nên \[\widehat {BEC} = \widehat {DCF}\]
Do \[BC\parallel DF\] nên \[\widehat {BCE} = \widehat {DFC} \Rightarrow \Delta BCE\~\Delta DFC\]
Suy ra \[\frac{{BE}}{{DC}} = \frac{{BC}}{{DF}}\] hay \[BE.DF = CD.BC\]
Mặt khác \[\widehat A = 60^\circ \Rightarrow \widehat C = 60^\circ \Rightarrow \Delta BCD\] đều
Do đó \[BE.DF = CD.BC = BD.BD = B{D^2}\] (đpcm)
Vậy \[BE.DF = B{D^2}\]
Câu 35:
Cho hình thoi ABCD có \[\widehat A = 60^\circ \]. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt đường thẳng AB tại E và cắt đường thẳng AD tại F.
Chứng minh \[\Delta BDE\sim\Delta DBF\]
 Xem đáp án
Xem đáp án
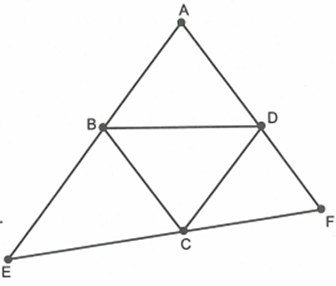
Từ \[BE.DF = B{D^2}\] suy ra \[\frac{{BE}}{{BD}} = \frac{{BD}}{{DF}}\]
Do \[\widehat A = 60^\circ \] nên \[\Delta ABD\] đều, và từ đó ta tính được \[\widehat {EBD} = \widehat {BDF} = 120^\circ \]
Xét \[\Delta BDE\] và \[\Delta DBF\] có: \[\frac{{BE}}{{BD}} = \frac{{BD}}{{DF}};\,\,\widehat {EBD} = \widehat {BDF}\] nên \[\Delta BDE\sim\Delta DFB\] (c.g.c) (đpcm).
Câu 36:
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Tính AC
 Xem đáp án
Xem đáp án
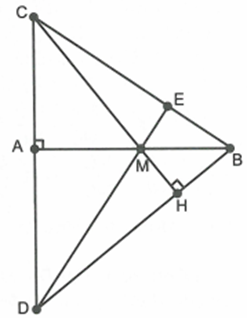
Áp dụng định lí Pitago cho tam giác vuông ABC ta có:
\[A{C^2} = B{C^2} - A{B^2} = {25^2} - {20^2} \Rightarrow AC = 15\]
Câu 37:
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Qua B vẽ đường thẳng vuông góc với CM tại H, cắt AC tại D. Chứng minh \[\Delta AMC\sim\Delta HMB\]
 Xem đáp án
Xem đáp án
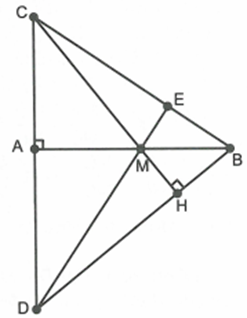
Xét \[\Delta AMC\] và \[\Delta HMB\] có: \[\widehat {MAC} = \widehat {MHB} = 90^\circ ;\,\,\widehat {AMC} = \widehat {HMB}\] (đối đỉnh) nên \[\Delta AMC\sim\Delta HMB\] (g.g)
Câu 38:
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Chứng minh \[AC.AD = AM.AB\]
 Xem đáp án
Xem đáp án
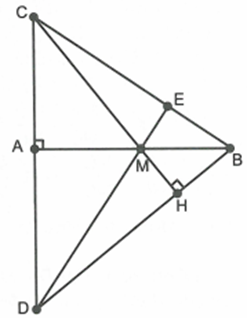
Do \[\Delta AMC\~\Delta HMB\] nên \[\widehat {MBH} = \widehat {ACM}\]
Xét \[\Delta ACM\] và \[\Delta ABD\] có: \[\widehat {CAM} = \widehat {BAD} = 90^\circ ;\,\,\widehat {ACM} = \widehat {ABD}\]
Nên \[\Delta ACM\~\Delta ABD\] (g.g)
Suy ra \[\frac{{AC}}{{AB}} = \frac{{AM}}{{AD}}\] hay \[AC.AD = AM.AB\]
Câu 39:
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Chứng minh \[DM \bot BC\]
 Xem đáp án
Xem đáp án
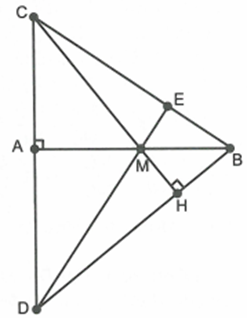
Tam giác CBD có hai đường cao CH, BA cắt nhau tại M nên DM là đường cao và do đó \[DM \bot BC\]
Câu 40:
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Tính BD và CD
 Xem đáp án
Xem đáp án
Áp dụng định lí Pitago vào tam giác vuông ABC ta tính được \[BC = 8\]
Theo tính chất đường phân giác và tính chất của dãy tỉ lệ thức bằng nhau ta có:
\[\frac{{BD}}{{AB}} = \frac{{CD}}{{AC}} = \frac{{BD + CD}}{{AB + AC}} = \frac{{BC}}{{AB + AC}} = \frac{8}{{16}}\]
Từ đó ta tính được \[BD = 3,\,\,CD = 5\]
Câu 41:
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
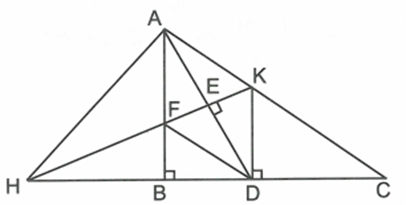
Qua D kẻ đường thẳng vuông góc với BC cắt AC tại K. Qua K kẻ đường thẳng vuông góc với AD cắt AD, AB, BC lần lượt tại E, F, H. Chứng minh \[\Delta ABC\sim\Delta HDK\]
 Xem đáp án
Xem đáp án
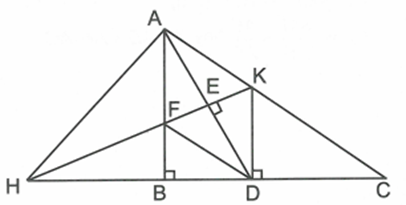
Do AB, DK cùng vuông góc với BC nên \[AB\parallel DK\]. Suy ra \[\widehat {BAD} = \widehat {ADK}\]
Mặt khác, \[\widehat {ADK} = \widehat {KHD}\] (cùng phụ với \[\widehat {HKD}\]). Do đó \[\widehat {BAD} = \widehat {KHD}\]
Xét \[\Delta ABD\] và \[\Delta HDK\] có: \[\widehat {BAD} = \widehat {KHD};\,\,\widehat {ABD} = \widehat {HDK} = 90^\circ \] nên \[\Delta ABD\sim\Delta HDK\] (g.g)
Câu 42:
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Chứng minh \[AK\parallel DF\]
 Xem đáp án
Xem đáp án
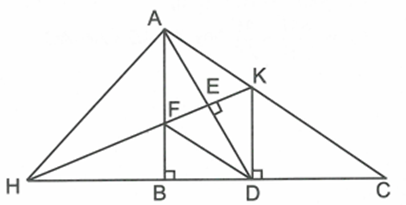
\[\Delta AFK\] có AE vừa là đường cao, vừa là đường phân giác nên cân tại A và E là trung điểm của FK (1)
\[ \Rightarrow \widehat {AFK} = \widehat {AKF}\]. Mà \[\widehat {AFK} = \widehat {DKF}\,\,(AB\parallel DK)\] nên suy ra \[\widehat {AKF} = \widehat {DKF}\]
\[ \Rightarrow \Delta AKD\] cân tại K và E là trung điểm của AD (2)
Từ (1) và (2), suy ra tứ giác AKDF có hai đường chéo AD và FK cắt nhau tại trung điểm của mỗi đường nên AKDF là hình bình hành.
Do vậy \[AK\parallel DF\]
Câu 43:
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Chứng minh \[\Delta CHA\] vuông tại A
 Xem đáp án
Xem đáp án
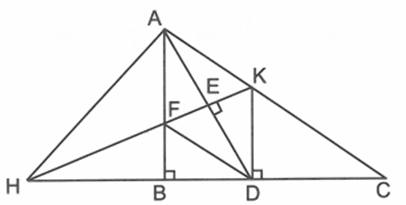
Xét tam giác AHD có HE vừa là đường cao, vừa là đường trung tuyến nên tam giác AHD cân và \[\widehat {AHE} = \widehat {DHE}\]
Xét \[\Delta AHK\] và \[\Delta DHK\] có: \[\widehat {AHE} = \widehat {DHE}\]; cạnh HK chung; \[\widehat {AKH} = \widehat {DKH}\] nên \[\Delta AHK = \Delta DHK\] (g.c.g). Từ đó suy ra \[\widehat {HAK} = \widehat {HDK} = 90^\circ \]
Vậy \[\Delta AHC\] vuông tại A.
Câu 44:
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Chứng minh \[\frac{{CH}}{{AH}} = \frac{{KD}}{{BF}}\]
 Xem đáp án
Xem đáp án
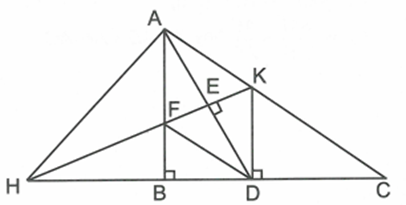
Xét \[\Delta ABH\] và \[\Delta CAH\] có: \[\widehat {ABH} = \widehat {CAH} = 90^\circ ;\,\,\widehat {AHB}\] chung nên \[\Delta ABH\~\Delta CAH\] (g.g)
\[ \Rightarrow \frac{{AH}}{{HC}} = \frac{{BH}}{{AH}} \Rightarrow \frac{{CH}}{{AH}} = \frac{{AH}}{{BH}} = \frac{{HD}}{{BH}} = \frac{{DK}}{{BF}}\]
Vậy \[\frac{{CH}}{{AH}} = \frac{{KD}}{{BF}}\]
Câu 45:
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[\Delta ABC\sim\Delta DBE\]
 Xem đáp án
Xem đáp án
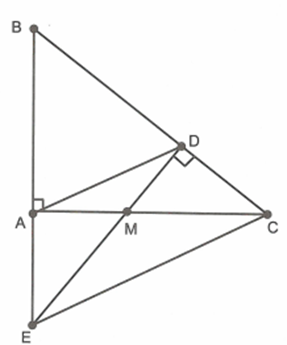
Xét \[\Delta ABC\] và \[\Delta DBE\] có: \[\widehat B\] chung; \[\widehat A = \widehat D = 90^\circ \] nên \[\Delta ABC\sim\Delta DBE\] (g.g)
Câu 46:
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[MA.MC = MD.ME\]
 Xem đáp án
Xem đáp án
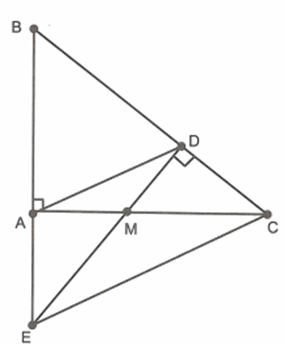
Xét \[\Delta MAE\] và \[\Delta MDC\] có: \[\widehat {MAE} = \widehat {MDC} = 90^\circ ;\,\,\widehat {AME} = \widehat {DMC}\] (đối đỉnh) nên \[\Delta MAE\~\Delta MDC\] (g.g)
Từ đó suy ra \[\frac{{MA}}{{MD}} = \frac{{ME}}{{MC}}\] hay \[MA.MC = MD.ME\]
Câu 47:
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[\Delta MAD\sim\Delta MEC\]
 Xem đáp án
Xem đáp án
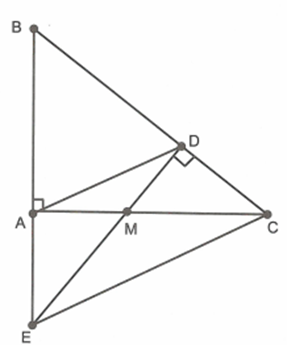
Từ \[\frac{{MA}}{{MD}} = \frac{{ME}}{{MC}}\] suy ra \[\frac{{MA}}{{ME}} = \frac{{MD}}{{MC}}\]
Xét \[\Delta MAD\] và \[\Delta MEC\] có: \[\frac{{MA}}{{ME}} = \frac{{MD}}{{MC}};\,\,\widehat {AMD} = \widehat {CME}\] (đối đỉnh) nên \[\Delta MAD\sim\Delta MEC\] (c.g.c)
Câu 48:
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[AB.AE = AM.AC\]
 Xem đáp án
Xem đáp án
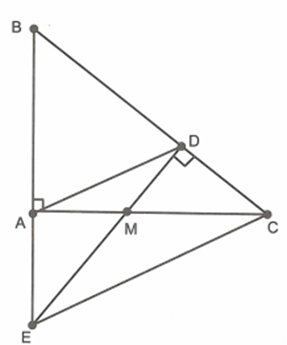
Do \[\Delta MAD\~\Delta MEC\] nên \[\widehat E = \widehat C\]
Xét \[\Delta AME\] và \[\Delta ABC\] có: \[\widehat E = \widehat C;\,\,\widehat {BAC} = \widehat {EAM} = 90^\circ \] nên \[\Delta AME\~\Delta ABC\] (g.g)
Suy ra \[\frac{{AM}}{{AB}} = \frac{{AE}}{{AC}}\] hay \[AB.AE = AM.AC\].
