Xét các mệnh đề sau:

I). Hàm số $y=-{(x-1)}^3$ nghịch biến trên R.

(II). Hàm số  đồng biến trên tập xác định của nó.

(III). Hàm số  đồng biến trên R.

Hỏi có bao nhiêu mệnh đề đúng?

I. Tính đơn điệu của hàm số

1. Nhắc lại định nghĩa

- Định nghĩa:

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:

Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) nhỏ hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) < f(x₂).

Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) lớn hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) > f(x₂).

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

- Nhận xét: Từ định nghĩa trên ta thấy:

a) f(x) đồng biến trên K $\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0;\forall x_1;x_2\in K;(x_1\ne x_2)$.

f(x) nghịch biến trên K $\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}<\mathrm{\hspace{0.17em}0};\forall x_1;x_2\in K;(x_1\ne x_2)$.

b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

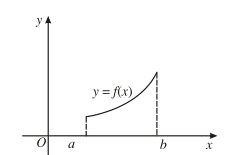
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

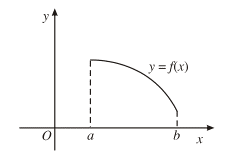
2. Tính đơn điệu và dấu của đạo hàm

- Định lí:

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

- Chú ý:

Nếu f’(x) = 0 với $\forall x\in K$ thì f(x) không đổi trên K.

Ví dụ 1. Tìm các khoảng đơn điệu của hàm số

a) y = x² + 2x – 10;

b) $y=\frac{x+\mathrm{\hspace{0.17em}5}}{2x-3}$.

Lời giải:
a) Hàm số đã cho xác định với mọi x$\in R$.

Ta có  đạo hàm y’ = 2x + 2

Và y’ = 0 khi x = – 1.

Lập bảng biến thiên:

 Vậy hàm số đã cho đồng biến trên khoảng $(-1;+\mathrm{\infty })$ và  nghịch biến trên khoảng $(-\mathrm{\infty };-1)$.

b) $y=\frac{x+\mathrm{\hspace{0.17em}5}}{2x-3}$

Hàm số đã cho xác định với $\forall x\ne \frac{3}{2}$

Ta có: $y^{\text{'}}=\frac{-13}{{(2x-3)}^2}<0\forall x\ne \frac{3}{2}$

Do đó, hàm số đã cho nghịch biến trên khoảng $(-\mathrm{\infty };\frac{3}{2})$ và $(\frac{3}{2};+\mathrm{\infty })$.

 - Chú ý:

Ta có định lí mở rộng sau đây:

Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu $f^{\text{'}}\left(x\right)\ge 0(f^{\text{'}}\left(x\right)\le 0);\forall x\in K$

Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

Ví dụ 2.  Tìm các khoảng đơn điệu của hàm số y = x³ – 6x² + 12x – 10.

Lời giải:

Hàm số đã cho xác định với mọi x$\in R$.

Ta có: y’ = 3x² – 12x + 12 = 3(x – 2)²

Do đó; y’ = 0 khi x = 2 và y’ > 0 với $\forall x\ne 2$.

Theo định lí mở rộng, hàm số đã cho luôn luôn đồng biến trên \(\mathbb{R}\).

II. Quy tắc xét tính đơn điệu của hàm số.

1. Quy tắc

- Bước 1. Tìm tập xác định.

- Bước 2. Tính đạo hàm  f’(x). Tìm các điểm x_i  ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

- Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

- Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

2. Áp dụng

Ví dụ 3. Xét sự đồng biến, nghịch biến của hàm số y = x⁴ – 2x² – 3.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = 4x³ – 4x

y’ = 0 $\iff [\begin{array}{c}x=0\\ x=\pm 1\end{array}$

Bảng biến thiên:

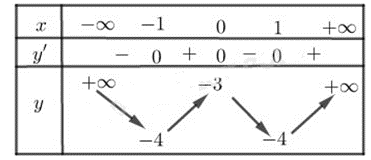
Vậy hàm số đã cho đồng biến trên (– 1; 0) và $(1;+\mathrm{\infty })$

Hàm số nghịch biến trên $(-\mathrm{\infty };-1)$ và (0; 1).

Ví dụ 4.  Cho hàm số $y=-x^3+6x^2-\mathrm{\hspace{0.17em}\hspace{0.17em}9}x+\mathrm{\hspace{0.17em}3}$. Xét tính đồng biến, nghịch biến của hàm số trên.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = – 3x² + 12x – 9

Và y’ = 0 $\iff [\begin{array}{c}x=\mathrm{\hspace{0.17em}\hspace{0.17em}1}\\ x=\mathrm{\hspace{0.17em}3}\end{array}$

Bảng biến thiên:

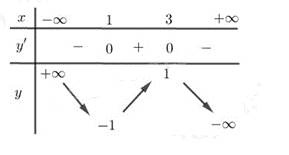
Vậy hàm số đã cho đồng biến trên (1; 3); nghịch biến trên $(-\mathrm{\infty };\mathrm{\hspace{0.17em}\hspace{0.17em}1})$ và $(3;+\mathrm{\infty })$.