Cho ∆MNP vuông tại M có MN dài hơn MP 10 cm. Biết chu vi của ∆MNP là 50 cm. Độ dài của cạnh NP bằng khoảng:
A. 21,41 cm;
B. 11,5 cm;
C. 28,71 cm;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Theo đề, ta có MN dài hơn MP 10 cm nên MN = MP + 10.
Xét ∆MNP vuông tại M có MN2 + MP2 = NP2 (Định lí Pythagore)
Suy ra (MP + 10)2 + MP2 = NP2
Hay MP2 + 20MP + 100 + MP2 = NP2
Do đó NP2 = 2MP2 + 20MP + 100
Nên
• Ta có chu vi của ∆MNP là 50 cm.
Suy ra: MN + NP + MP = 50.
Khi đó
(1)
Bình phương hai vế của phương trình trên ta được:
2MP2 + 20MP + 100 = 1600 – 160MP + 4MP2
Þ 2MP2 – 180MP + 1500 = 0
Þ MP ≈ 80,71 hoặc MP ≈ 9,29.
Thay lần lượt các giá trị trên vào phương trình (1), ta thấy chỉ có MP ≈ 9,29 thỏa mãn.
Do đó NP ≈ 21,41 cm.
Vậy ta chọn phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Khoảng cách từ nhà An ở vị trí A đến nhà Bình là 200 m. Từ nhà, nếu An đi x mét theo phương tạo với AB một góc 120° thì sẽ đến nhà bác Mai ở vị trí M và nếu đi thêm 300 m nữa thì sẽ đến siêu thị ở vị trí S.
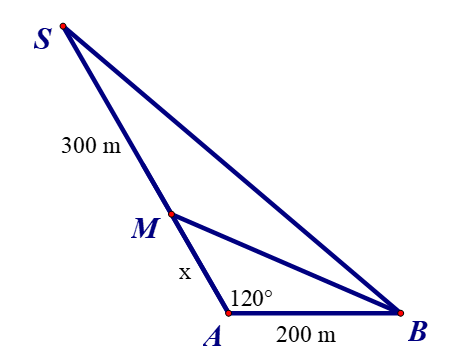
Biết rằng quãng đường từ nhà Bình đến siêu thị gấp đôi quãng đường từ nhà Bình đến nhà bác Mai. Khi đó quãng đường từ nhà An đến nhà bác Mai là:
Cho phương trình . Biết phương trình đã cho có một nghiệm có dạng , với là phân số tối giản và b > 0. Khi đó giá trị biểu thức a2 – b2 bằng:
Bài 3: Phương trình quy về phương trình bậc hai