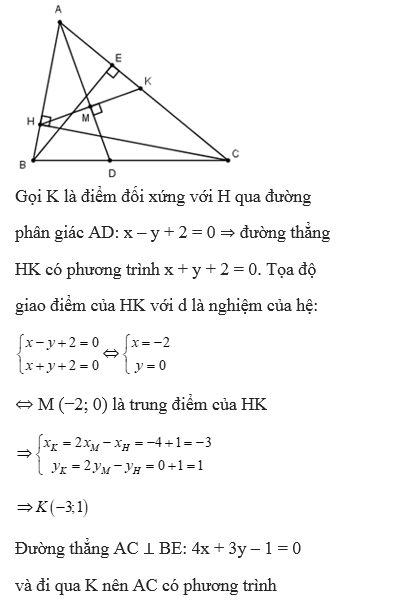
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có hình chiếu của C trên đường thẳng AB là H (−1; −1), đường thẳng chứa phân giác của góc A có phương trình x – y + 2 = 0 và đường cao kẻ từ B có phương trình 4x + 3y – 1 = 0. Tìm tọa độ điểm C.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng 2
Phương trình đường tròn (C) đi qua A (3; 3) và tiếp xúc với đường thẳng (d): 2x + y – 3 = 0 tại điểm B (1; 1) là:
Cho đường tròn (C): x2 + y2 + 6x − 2y + 5 = 0 và điểm A (−4; 2). Đường thẳng d qua A cắt (C) tại 2 điểm M, N sao cho A là trung điểm của MN có phương trình là
Cho (E) có hai tiêu điểm F1 (−4; 0), F2 (4; 0) và điểm M thuộc (E). Biết chu vi tam giác MF1F2 bằng 18. Khi đó tâm sai của (E) bằng
Cho đường thẳng (Δ): 3x − 2y + 1 = 0. Viết PTĐT (d) đi qua điểm M (1; 2) và tạo với (Δ) một góc 450
Phương trình đường tròn tâm I thuộc đường thẳng d có phương trình x − 2y + 5 = 0 và đi qua hai điểm A (0; 4), B (2; 6) là:
Cho (E) có hai tiêu điểm và điểm M () thuộc (E). Gọi N là điểm đối xứng với M qua gốc tọa độ O. Khi đó:
Một miếng giấy hình tam giác ABC vuông tại A có diện tích S, gọi I là trung điểm BC và O là trung điểm của AI. Cắt miếng giấy theo một đường thẳng qua O, đường thẳng này đi qua M, N lần lượt trên các cạnh AB, AC. Khi đó diện tích miếng giấy chứa điểmA có diện tích thuộc đoạn:
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C): x2 + y2 + 2x − 8y – 8 = 0. Phương trình đường thẳng Δ nào dưới đây song song với đường thẳng 3x + 4y – 2 = 0 và cắt đường tròn (C) theo dây cung có độ dài 6?
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại đỉnh A (6; 6), đường thẳng đi qua trung điểm của các cạnh AB và AC có phương trình x + y – 4 = 0. Có bao nhiêu cặp điểm B, C thỏa mãn yêu cầu bài toán, biết điểm E (1; −3) nằm trên đường cao đi qua đỉnh C của tam giác đã cho.
Đường thẳng đi qua M ( 1; ) và tạo với chiều trục Ox một góc bằng 600 có phương trình là:
Phương trình đường tròn (C) có bán kính lớn nhất đi qua M (4; 2) và tiếp xúc với 2 trục tọa độ là:
Phương trình đường tròn (C) ngoại tiếp tam giác ABC có 3 cạnh nằm trên 3 đường thẳng 3y = x, y = x + 2, y = 8 − x là:
Cho hai điểm A (3; 0), B (0; 4). Phương trình đường tròn (C) có bán kính nhỏ nhất nội tiếp tam giác OAB là: