Một đám vi khuẩn tại ngày thứ t có số lượng là N(t). Biết rằng và lúc đầu đám vi khuẩn có 250000 con. Sau 10 ngày số lượng vi khuẩn xấp xỉ bằng:
A. 264334.
B. 263334.
C.264254.
D.254334.
 Giải bởi Vietjack
Giải bởi Vietjack
Số lượng vi khuẩn tại ngày thứ t bằng
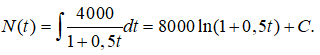
Với t = 0 ta có: N(0) = C = 250000,
Vậy N(t) = 8000.ln(1 + 0,5t) + 250000
khi đó N(10) = 8000.ln(1 + 0,5.10) + 250000 ≈ 264334.
Chọn đáp án A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x - sin2x ?
Trong các hàm số sau hàm số nào không phải là một nguyên hàm của f(x) = cosxsinx ?
Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc . Vận tốc ban đầu của vật là 6m/s. Vận tốc của vật sau 10 giây xấp xỉ bằng
Cho các hàm số: ; F(x)= với Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
1. Nguyên hàm.
- Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi .
Ví dụ 1.
- Hàm số F(x) = sinx + 6 là một nguyên hàm của hàm số f(x) = cosx trên khoảng vì F’(x) = (sinx + 6)’ = cosx với .
- Hàm số là một nguyên hàm của hàm số trên khoảng
Vì với .
- Định lí 1.
Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Định lí 2.
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó là họ tất cả các nguyên hàm của f(x) trên K.
Kí hiệu: .
- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.
Ví dụ 2.
a) Với ta có: ;
b) Với ta có: ;
c) Với ta có: .
2. Tính chất của nguyên hàm
- Tính chất 1.
Ví dụ 3.
- Tính chất 2.
(k là hằng số khác 0).
- Tính chất 3.
.
Ví dụ 4. Tìm nguyên hàm của hàm số trên khoảng .
Lời giải:
Với ta có:
Định lí:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Ví dụ 5.
a) Hàm số có nguyên hàm trên khoảng .
b) Hàm số y = có nguyên hàm trên khoảng
4. Bảng nguyên hàm của một số hàm số thường gặp
Ví dụ 6. Tính:
a)
b)
Lời giải:
a)
- Chú ý: Từ đây, yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.
II. Phương pháp tính nguyên hàm.
- Định lí 1.
Nếu và u = u(x) là hàm số có đạo hàm liên tục thì:
.
Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:
.
Ví dụ 7. Tính .
Lời giải:
Ta có: nên theo hệ quả ta có:
.
Chú ý:
Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).
Ví dụ 8. Tính .
Lời giải:
Đặt u = cosx. Suy ra: du = – sinx. dx
Khi đó, nguyên hàm đã cho trở thành:
Thay u = cosx vào kết quả ta được:
2. Phương pháp tính nguyên hàm từng phần.
- Định lí 2.
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
.
- Chú ý.
Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:
.
Đó là công thức nguyên hàm từng phần.
Ví dụ 9. Tính
a) ;
b) ;
c)
Lời giải:
a)
Đặt
Ta có:
.
b) ;
Đặt
Khi đó:
c)
Đặt
Khi đó: