Cho hình lập phương ABCD.A'B'C'D' cạnh a. Hình nào dưới đây bằng hình lăng trụ ABC.A'B'C'?
A. AA'D'.BB'C'
B. ABCD.A'B'C'D'
C. C'.CDAB
D. B.ACC'A'
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S. ABCD có đáy là hình vuông, SA vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi. Hình nào sau đây bằng hình chóp B'.ABC?
Cho khối đa diện có các mặt đều là tam giác. Kí hiệu số mặt là M, số cạnh là C. Chọn mệnh đề đúng:
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Hình nào dưới đây bằng hình chóp A'.ABCD?
Cho khối đa diện mà mỗi đỉnh là đỉnh chung của 3 cạnh. Kí hiệu D là số đỉnh, C là số cạnh. Chọn mệnh đề đúng:
Nếu có phép đối xứng qua mặt phẳng biến hình lập phương ABCD.A'B'C'D' thành hình lập phương MNPQ.M’N’P’Q’ thì
Cho điểm , gọi B’ là ảnh của B qua phép đối xứng qua mặt phẳng (P), . Chọn kết luận đúng:
Cho tứ diện ABCD có ba mặt ABC, ACD, ADB là ba tam giác bằng nhau và cân tại đỉnh A. Số mặt phẳng đối xứng của tứ diện đó là:
I. Khối lăng trụ và khối chóp.
- Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
- Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
Ví dụ 1. Ứng với hình lăng trụ tứ giác ABCD.EFGH ta có khối lăng trụ tứ giác ABCD.EFGH; ứng với hình chóp tứ giác S.ABCD ta có khối chóp tứ giác S.ABCD.
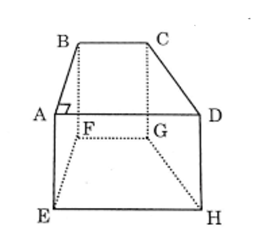
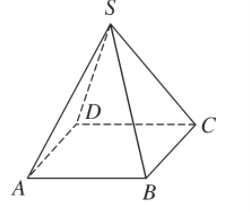
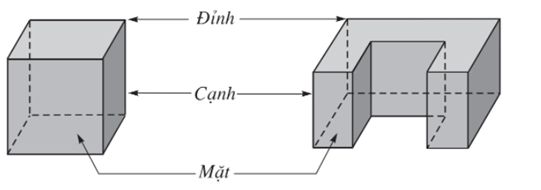
- Ta gọi đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của một hình lăng trụ (hình chóp hay hình chóp cụt) theo thứ tự là đỉnh; cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của khối lăng trụ (khối chóp hay khối chóp cụt) tương ứng.
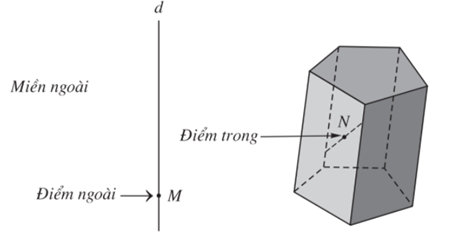
- Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự.
II. Khái niệm về hình đa diện và khối đa diện
1. Khái niệm về hình đa diện
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
- Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là đỉnh, cạnh của hình đa diện.
2. Khái niệm về khối đa diện
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
Ví dụ 2.
- Các hình dưới đây là những khối đa diện
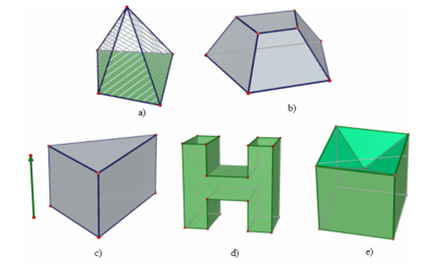
- Các hình dưới đây không phải là những khối đa diện.
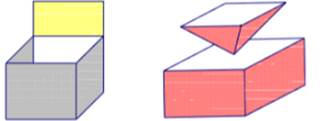
III. Hai đa diện bằng nhau.
1. Phép dời hình trong không gian.
- Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian.
- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
- Ví dụ 3. Trong không gian, các phép biến hình sau đây gọi là phép dời hình :
a) Phép tịnh tiến theo vectơ , là phép biến hình, biến mỗi điểm M thành điểm M’ sao cho
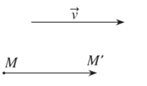
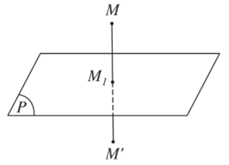
b) Phép đối xứng qua mặt phẳng (P), là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.
Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
c) Phép đối xứng tâm O, là phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm của MM’.
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).
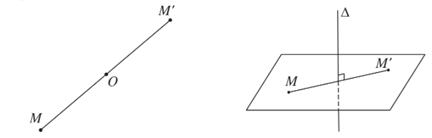
d) Phép đối xứng qua đường thẳng ∆ (hay phép đối xứng qua trục ∆) là phép biến hình biến mọi điểm thuộc đường thẳng ∆ thành chính nó, biến mỗi điểm M không thuộc ∆ thành điểm M’ sao cho ∆ là đường trung trực của MM’.
Nếu phép đối xứng qua đường thẳng ∆ biến hình (H) thành chính nó thì ∆ gọi là trục đối xứng của (H) .
Nhận xét:
+ Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
+ Phép dời hình biến đa diện (H) thành đa diện (H’), biến đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của (H’).
2. Hai hình bằng nhau
- Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt, hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
- Ví dụ 4. Phép đối xứng tâm O biến đa diện (H) thành đa diện (H’). Phép đối xứng trục ∆, biến đa diện (H’) thành đa diện (H”). Do đó, phép dời hình có được bằng cách thực hiện liên tiếp hai phép dời hình trên biến hình (H) thành hình (H”) .
Từ đó, suy ra các hình (H); (H’) và (H”) là bằng nhau.
IV. Phân chia và lắp ghép các khối đa diện
Nếu khối đa diện (H) là hợp của hai khối đa diện (H1) và (H2) sao cho (H1) và (H2) không có chung điểm trong nào thì ta nói có thể chia được khối đa diện (H) thành hai khối đa diện (H1) và (H2), hay có thể lắp ghép hai khối đa diện (H1) và (H2) với nhau để được khối đa diện (H).
- Ví dụ 5. Với khối chóp tứ giác S.ABCD, ta hãy xét hai khối chóp tam giác S.ABC và S.ACD.
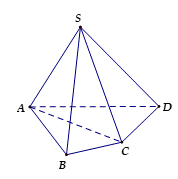
Ta thấy rằng:
+ Hai khối chóp S.ABC và S.ACD không có điểm trong chung.
+ Hợp của hai khối chóp S.ABC và S.ACD chính là khối chóp S.ABCD.
Vậy khối chóp S.ABCD được phân chia thành hai khối chóp tam giác là S.ABC và S.ACD .
- Nhận xét. Một khối đa diện bất kì luôn có thể phân chia thành những khối tứ diện.