Trong các tích phân sau, tích phân nào có giá trị bằng 2?

I. Khái niệm tích phân

1. Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

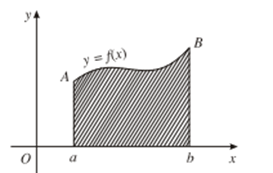
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a;  x = b (a < b); trục hoành và đường cong y = f(x),  trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in [a;b]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

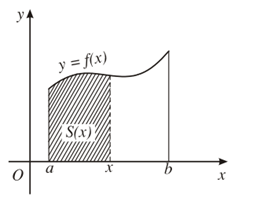
 Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) +  C.

Vì S(a) = 0 nên F(a) +  C = 0  hay C =  –  F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

2. Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$.

Ta còn dùng kí hiệu ${F\left(x\right)|}_a^b$ để chỉ hiệu số F(b) – F(a).

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x={F\left(x\right)|}_a^b=F\left(b\right)-F\left(a\right)$.

Ta gọi $\underset{a}{\overset{b}{\int }}$là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

- Chú ý.

Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)𝑑x=0;\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x=-\underset{b}{\overset{a}{\int }}f\left(x\right)𝑑x$.

Ví dụ 1.

a) $\underset{0}{\overset{2}{\int }}(x+2)𝑑x={(\frac{x^2}{2}+\mathrm{\hspace{0.17em}\hspace{0.17em}2}x)|}_0^2=\mathrm{\hspace{0.17em}6}-0=6$;

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}(2+\cos x)𝑑x={(2x+\sin x)|}_0^{\frac{\pi }{2}}=(\pi \mathrm{ }+1)-0=\pi +\mathrm{\hspace{0.17em}1}$.                           

- Nhận xét.

a) Tích phân của hàm số f từ a đến b có thể kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$ hay $\underset{a}{\overset{b}{\int }}f\left(t\right)𝑑t$. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.

b) Ý nghĩa hình học của tích phân.

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$ là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy $S=\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$.

II. Tính chất của tích phân.

- Tính chất 1:

$\underset{a}{\overset{b}{\int }}k.f\left(x\right)dx=k.\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$  (k là hằng số).

- Tính chất 2:

$\underset{a}{\overset{b}{\int }}[f\left(x\right)\pm g\left(x\right)]𝑑x=\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x\pm \underset{a}{\overset{b}{\int }}g\left(x\right)𝑑x$.

Ví dụ 2.  Tính: $\underset{0}{\overset{\pi }{\int }}(3x-\mathrm{\hspace{0.17em}4}\sin x)𝑑x$.

Lời giải:

Ta có:

  $\begin{array}{c}\underset{0}{\overset{\pi }{\int }}(3x-\mathrm{\hspace{0.17em}4}\sin x)𝑑x=\mathrm{\hspace{0.17em}\hspace{0.17em}3}\underset{0}{\overset{\pi }{\int }}\mathrm{ }x𝑑x-\mathrm{\hspace{0.17em}4}\underset{0}{\overset{\pi }{\int }}\sin xdx=\mathrm{\hspace{0.17em}\hspace{0.17em}3}.{\frac{x^2}{2}|}_0^{\pi }+{4c\mathrm{osx}|}_0^{\pi }=\frac{3{\pi }^2}{2}+(-4-4)=\frac{3{\pi }^2}{2}-\mathrm{\hspace{0.17em}\hspace{0.17em}8}\end{array}$

- Tính chất 3.

$\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x=\underset{a}{\overset{c}{\int }}f\left(x\right)𝑑x+\underset{c}{\overset{b}{\int }}f\left(x\right)𝑑x$      (a < c < b).

Ví dụ 3. Tính $\underset{-2}{\overset{2}{\int }}\left|x\right|𝑑x$.

Lời giải:

Ta có: $\left|x\right|=\{\begin{array}{c}-x khi-2\le x\le 0\\ x khi\mathrm{\hspace{0.17em}\hspace{0.17em}0}\le x\le 2\end{array}$

Do đó; $\underset{-2}{\overset{2}{\int }}\left|x\right|𝑑x=\underset{-2}{\overset{0}{\int }}\left|x\right|𝑑x+\underset{0}{\overset{2}{\int }}\left|x\right|𝑑x$

$\begin{array}{c}=-\underset{-2}{\overset{0}{\int }}x𝑑x+\underset{0}{\overset{2}{\int }}x𝑑x={\frac{-x^2}{2}|}_{-2}^0+{\frac{x^2}{2}|}_0^2=(0+\mathrm{\hspace{0.17em}2})+(2-0)=4\end{array}$

III. Phương pháp tính tích phân

1. Phương pháp đổi biến số

- Định lí:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $[\alpha ;\beta ]$ sao cho $\phi \left(\alpha \right)=a;\phi \left(\beta \right)=b$.

Khi đó: $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x=\underset{\alpha }{\overset{\beta }{\int }}\mathrm{ }f(\phi \left(t\right)).{\phi }^{\text{'}}\left(t\right)dt$.

Ví dụ 4.  Tính $\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}𝑑x$.

Lời giải:

Đặt x = sint; suy ra: dx = costdt.

Đổi cận:

$\begin{array}{c}x=\mathrm{\hspace{0.17em}0}\Rightarrow t=\mathrm{\hspace{0.17em}\hspace{0.17em}0}\\ x=\mathrm{\hspace{0.17em}1}\Rightarrow t=\frac{\pi }{2}\end{array}$

Ta có:

 $\begin{array}{c}\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}𝑑x=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{1-{\sin }^{2}t}.c\mathrm{ostdt}=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sqrt{{\cos }^{2}t}.c\mathrm{ost}.\mathrm{dt}=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\mathrm{cost}.c\mathrm{ost}.\mathrm{dt}\end{array}$

$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^{2}tdt=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{2}(1+c\mathrm{os}2t)𝑑t$

$=\frac{1}{2}.{(t+\frac{\sin 2t}{2})|}_0^{\frac{\pi }{2}}=\frac{\pi }{4}-\mathrm{\hspace{0.17em}0}=\frac{\pi }{4}.$

- Chú ý:

Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x$, đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và $u\left(x\right)\in [\alpha ;\beta ]$.

Giả sử có thể viết: f(x) = g(u(x)). u’(x) với $x\in [a;b]$ với g(u) liên tục trên đoạn $[\alpha ;\beta ]$.

Khi đó, ta có: $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x=\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)𝑑u$.

 Ví dụ 5. Tính $\underset{0}{\overset{\sqrt{\pi }\mathrm{ }}{\int }}x.\sin x^{2}dx$.

Lời giải:

Đặt t = x². Suy ra: dt = 2xdx $\Rightarrow xdx=\frac{dt}{2}$

Đổi cận:

Ta có:

  $\underset{0}{\overset{\sqrt{\pi }}{\int }}x.\sin x^{2}dx=\underset{0}{\overset{\pi }{\int }}\sin t.\frac{dt}{2}$

$=\frac{1}{2}\underset{0}{\overset{\pi }{\int }}\sin t.dt={\frac{1}{2}(-c\mathrm{ost})|}_0^{\pi }=\frac{1}{2}-\left(\frac{-1}{2}\right)=1.$

2. Phương pháp tính tích phân từng phần

- Định lí.

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

$\underset{a}{\overset{b}{\int }}u\left(x\right).v^{\text{'}}\left(x\right)dx=[u\left(x\right).v\left(x\right)]{|}_a^b-\underset{a}{\overset{b}{\int }}v\left(x\right).u^{\text{'}}\left(x\right)dx$

Hay $\underset{a}{\overset{b}{\int }}u𝑑v={uv|}_a^b-\underset{a}{\overset{b}{\int }}v𝑑u$.

Ví dụ 6. Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}x\sin xdx.$

Lời giải:

Đặt $\{\begin{array}{c}u=x\\ dv=\sin xdx\end{array}$

Do đó  $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}x\sin xdx\mathrm{ }={(-x\cos x)|}_0^{\frac{\pi }{2}}+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\cos xdx\mathrm{ }=0+{\sin x|}_0^{\frac{\pi }{2}}=1.$

Ví dụ 7. Tính $I=\underset{0}{\overset{e-1}{\int }}x\ln (x+1)𝑑x$.

Lời giải:

Đặt $\{\begin{array}{c}u=\ln (x+1)\\ dv=xdx\end{array}$ ta có $\{\begin{array}{c}du=\frac{1}{x+1}\\ dx =\frac{x^2-1}{2}\end{array}$

$\begin{array}{c}I=\underset{0}{\overset{e-1}{\int }}x\ln (x+1)dx\mathrm{ }=\left[\ln (x+1)\frac{x^2-1}{2}\right]{|}_0^{e-1}-\frac{1}{2}\underset{0}{\overset{e-1}{\int }}(x-1)dx=\frac{e^2-2e}{2}-\frac{1}{2}(\frac{x^2}{2}-x){|}_0^{e-1}\end{array}$

$=\frac{e^2-2e}{2}-\frac{1}{2}.\frac{e^2-4e+3}{2}=\frac{e^2-3}{4}.$