Cho khối chóp S.ABCD có thể tích bằng , đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD. Biết diện tích tam giác SAB bằng . Tính khoảng cách từ M tới mặt phẳng (SAB)
A. 12a
B. 6a
C. 3a
D. 4a
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A, . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
Cho tứ diện ABCD có thể tích bằng 18. Gọi là trọng tâm của tam giác BCD; (P) là mặt phẳng qua A sao cho góc giữa (P) và mặt phẳng (BCD) bằng . Các đường thẳng qua B, C, D song song với cắt (P) lần lượt tại . Thể tích khối tứ diện bằng?
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng . Thể tích của khối lăng trụ?
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SC = 3a và SC vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng:
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng . Thể tích khối chóp S.ABCD là:
Cho hình lập phương ABCD.A'B'C'D' có diện tích mặt chéo ACC’A’ bằng . Thể tích của khối lập phương ABCD.A’B’C’D’ bằng:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết . Thể tích khối chóp S.ABC là:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có dộ dài là a. Thể tích khối tứ diện S.BCD bằng:
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng , . Thể tích của khối chóp S.ABC bằng:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết SA=BC=a, thể tích khối chóp S.ABC bằng:
I. Khái niệm về thể tích của khối đa diện
Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H) = V(H1) + V(H2).
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
II. Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
Ví dụ 1. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ.
Lời giải:
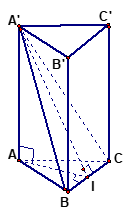
Gọi I là trung điểm BC .
Ta có; ∆ABC đều nên
Suy ra: (định lí 3 đường vuông góc)
Ta có:
Vì
Xét tam giác A’AI có :
Vậy : VABC.A’B’C’ = SABC .AA' =
III. Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là:
Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc 60o. Tính thể tích hình chóp.
Lời giải :

Gọi M là trung điểm của BC.
Vì tam giác ABC đều nên AM BC (định lí 3 đường vuông góc).
Vậy góc[(SBC);(ABC)] =
Tam giác ABC đều cạnh a nên đường cao
Xét tam giác SAM có : SA = AM.tan600 =
Vậy V =