Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là . Hai điểm A, B nằm trên đường tròn tâm O sao cho AB = 1/2. Tính thể tích khối tứ diện IABO
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
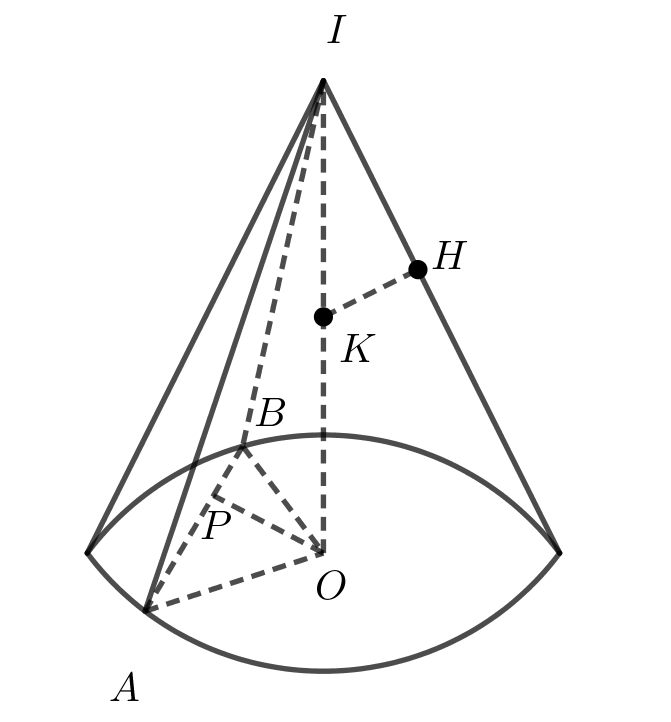
Gọi K là trung điểm của IO
Do bán kính đáy (r) = chiều cao hình nón (h)
nên tam giác thiết diện qua trục là tam giác vuông cân
Xét, có: OB = OA = 4; AB =
Nửa chu vi:
Khi đó, diện tích là:
Thể tích hình chóp IOAB là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp tứ giác đều S.ABCD, cạnh đáy là a, SA = 2a. Thể tích khối chóp là:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD
Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác đều cạnh a và hình chiếu vuông góc của đỉnh A’ trên mặt phẳng (ABC) là trung điểm cạnh BC. Thể tích khối chóp A.BCC’B’ là:
Cho hình chóp S.ABC có hình chiếu vuông góc của S lên mặt đáy là tâm O của đường tròn ngoại tiếp tam giác ABC. Biết SA = SB = a và góc giữa cạnh bên SA và mặt đáy bằng 60o. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC là:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu tâm B cắt SC theo một dây có độ dài là:
Trong không gian Oxyz, cho hai đường thẳng cắt nhau: : x = 1 + t, y = 1, z = 1 - t, : x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng ,
Cho một đồ chơi hình khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = 6cm. Trong tất cả các khối cầu có thể chứa đồ chơi đó thì khối cầu có bán kính nhỏ nhất là:
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
Trong không gian Oxyz, cho hai điểm A(3;2;1), M(3;0;0) và mặt phẳng (P) có phương trình là: x + y + z - 3 = 0. Viết phương trình của đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ A đến đường thẳng d lớn nhất
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC=a, SA = SB = SC = 3a. Góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp G.ABC là:
Có ba quả bóng đá hình cầu có cùng bán kính r được xếp tiếp xúc với nhau từng đôi một. Trong các rổ hình trụ có chiều cao 2r và bán kính R, hỏi bán kính R nhỏ nhất là bao nhiêu để hình trụ có thể chứa được cả ba quả bóng đó?