Gọi F(x) là nguyên hàm của hàm số $f\left(x\right)={\sin }^4\left(2x\right)$ thoả mãn F(0) = 3/8. Khi đó F(x) là:

1. Nguyên hàm và tính chất

1.1 Nguyên hàm.

- Định nghĩa

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R. 

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi $x\in K$.

Ví dụ.

- Hàm số F(x) = sinx + 6 là một nguyên hàm của hàm số f(x) = cosx trên khoảng $(-\mathrm{\infty };+\mathrm{\infty })$ vì F’(x) = (sinx + 6)’ = cosx với $\forall x\in (-\mathrm{\infty };+\mathrm{\infty })$.

- Hàm số $F\left(x\right)=\frac{x+\mathrm{\hspace{0.17em}2}}{x-3}$ là một nguyên hàm của hàm số $f\left(x\right)=\frac{-5}{{(x-3)}^2}$ trên khoảng $(-\mathrm{\infty };\mathrm{\hspace{0.17em}\hspace{0.17em}3})\cup (3;+\mathrm{\infty })$  

Vì $F^{\text{'}}\left(x\right)={\left(\frac{x+\mathrm{\hspace{0.17em}2}}{x-3}\right)}^{\text{'}}=\frac{-5}{{(x-3)}^2}=f\left(x\right)$ với $\forall x\in (-\mathrm{\infty };\mathrm{\hspace{0.17em}\hspace{0.17em}3})\cup (3;+\mathrm{\infty })$.

 - Định lí 1.

 Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

- Định lí 2.

Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F\left(x\right)+C;C\in R$ là họ tất cả các nguyên hàm của f(x) trên K.

Kí hiệu: $\int f\left(x\right)𝑑x=F\left(x\right)+C$ .

- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.

Ví dụ.

a) Với $x\in (-\mathrm{\infty };+\mathrm{\infty })$ ta có: ${\int x}^3𝑑x=\frac{x^4}{4}+C$;

b) Với $x\in (-\mathrm{\infty };+\mathrm{\infty })$ ta có: ${\int e}^x𝑑x=e^x+C$;

c) Với $x\in (0;+\mathrm{\infty })$ ta có: $\int \frac{1}{2\sqrt{x}}𝑑x=\sqrt{x}+C$.

1.2 Tính chất của nguyên hàm

- Tính chất 1.

${\int f}^{\text{'}}\left(x\right)𝑑x=f\left(x\right)+C$

Ví dụ.

$\int {\left(4^x\right)}^{\text{'}}𝑑x={\int 4}^x.\ln 4.dx={\mathrm{\hspace{0.17em}\hspace{0.17em}4}}^x+C$

- Tính chất 2.

$\int kf\left(x\right)𝑑x=k.\int f\left(x\right)𝑑x$  (k là hằng số khác 0).

- Tính chất 3.

$\int [f\left(x\right)\pm g\left(x\right)]𝑑x=\int f\left(x\right)𝑑x\pm \int g\left(x\right)𝑑x.$

Ví dụ. Tìm nguyên hàm của hàm số $f\left(x\right)=\mathrm{\hspace{0.17em}\hspace{0.17em}3}{x}^2+\mathrm{\hspace{0.17em}\hspace{0.17em}2}\sin x$ trên khoảng $(-\mathrm{\infty };+\mathrm{\infty }).$

Lời giải:

Với $x\in (-\mathrm{\infty };+\mathrm{\infty })$ ta có:

$\begin{array}{c}\int (3x^2+\mathrm{\hspace{0.17em}2}\sin x)𝑑x=\int 3x^2𝑑x+\mathrm{\hspace{0.17em}\hspace{0.17em}2}\int \sin xdx=x^3+\mathrm{\hspace{0.17em}2}.(-c\mathrm{osx})\mathrm{ }+\mathrm{C}\mathrm{ }=\mathrm{ }{\mathrm{x}}^3-2c\mathrm{osx}\mathrm{ }+\mathrm{C}\end{array}$

1.3 Sự tồn tại nguyên hàm

Định lí:

Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Ví dụ.

a) Hàm số $y=\sqrt{x}$ có nguyên hàm trên khoảng $(0;+\mathrm{\infty })$.

$\int \sqrt{x}𝑑x={\int x}^{\frac{1}{2}}𝑑x=\frac{2}{3}{x}^{\frac{3}{2}}+C=\frac{2}{3}x\sqrt{x}+C$

b) Hàm số y = $\frac{1}{x}$ có nguyên hàm trên khoảng $(-\mathrm{\infty };\mathrm{\hspace{0.17em}\hspace{0.17em}0})\cup (0;+\mathrm{\infty })$

$\int \frac{1}{x}𝑑x=\ln \left|x\right|+C$

1.4 Bảng nguyên hàm của một số hàm số thường gặp

Ví dụ. Tính:

a) $\int (3x^4+\sqrt[3]{x})𝑑x$

b) $\int (5e^x-{\mathrm{\hspace{0.17em}4}}^{x+\mathrm{\hspace{0.17em}2}})𝑑x$

Lời giải:

a)

 $\begin{array}{c}\int (3x^4+\sqrt[3]{x})𝑑x=\int 3x^4𝑑x+\int \sqrt[3]{x}𝑑x=\mathrm{\hspace{0.17em}\hspace{0.17em}3}\int x^4𝑑x+{\int x}^{\frac{1}{3}}𝑑x\end{array}$

$=\mathrm{\hspace{0.17em}\hspace{0.17em}3}.\frac{x^5}{5}+\frac{3}{4}.x^{\frac{4}{3}}+C=\frac{3x^5}{5}+\frac{3x\sqrt[3]{x}}{4}+C$

b) $\int (5e^x-{\mathrm{\hspace{0.17em}4}}^{x+\mathrm{\hspace{0.17em}2}})𝑑x$

$\begin{array}{c}=\mathrm{\hspace{0.17em}5}\int e^x𝑑x-\mathrm{\hspace{0.17em}\hspace{0.17em}16}.{\int \hspace{0.17em}4}^x𝑑x=\mathrm{\hspace{0.17em}\hspace{0.17em}5}.e^x-16.\frac{4^x}{\ln 4}+C\end{array}$

- Chú ý: Từ đây, yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.

2. Phương pháp tính nguyên hàm.

2.1  Phương pháp đổi biến số

- Định lí 1.

Nếu $\int f\left(u\right)𝑑u=F\left(u\right)+C$  và u = u(x) là hàm số có đạo hàm liên tục thì:

$\int f(u\left(x\right)).u^{\text{'}}\left(x\right)dx=F(u\left(x\right))+C.$

Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:

$\int f(ax+b)𝑑x=\frac{1}{a}F(ax+b)+C.$

Ví dụ. Tính $\int {(3x+\mathrm{\hspace{0.17em}2})}^3𝑑x.$

Lời giải:

Ta có: ${\int u}^3𝑑u=\frac{u^4}{4}+C$ nên theo hệ quả ta có:

$\int {(3x+\mathrm{\hspace{0.17em}2})}^3𝑑x=\frac{{(3x+2)}^4}{4}+C.$

Chú ý:

Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).

Ví dụ. Tính $\int \sin x.c{\mathrm{os}}^{2}xdx.$

Lời giải:

Đặt u = cosx. Suy ra: du = – sinx. dx

Khi đó, nguyên hàm đã cho trở thành:

${\int u}^2.(-du)=\mathrm{ }-{\int u}^2𝑑u\mathrm{ }=-\frac{u^3}{3}+C$

Thay u = cosx vào kết quả ta được:

$\int \sin x.c{\mathrm{os}}^{2}xdx=\frac{-c{\mathrm{os}}^{3}x}{3}+C.$

2.2 Phương pháp tính nguyên hàm từng phần.

- Định lí 2.

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

$\int u\left(x\right).v^{\text{'}}\left(x\right).dx=u\left(x\right).v\left(x\right)-\int u^{\text{'}}\left(x\right).v\left(x\right)dx.$

- Chú ý.

Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:

Đó là công thức nguyên hàm từng phần.

Ví dụ. Tính

a) $\int x\ln xdx$;

b) $\int x\sin xdx$;

c) $\int (5-x).e^{x}dx$

Lời giải:

a) $\int x\ln xdx$

Đặt $\{\begin{array}{c}u=\ln x\\ dv=xdx\end{array}\Rightarrow \{\begin{array}{c}du=\frac{1}{x}dx\\ v=\frac{x^2}{2}\end{array}$

Ta có:

 $\int x\ln xdx=\frac{x^2}{2}.\ln x-\int \frac{x^2}{2}.\frac{1}{x}dx$

$=\frac{x^2}{2}.\ln x-\frac{1}{2}\int x𝑑x=\frac{x^2}{2}.\ln x-\frac{1}{2}.\frac{x^2}{2}+C$

$=\frac{x^2}{2}.\ln x-\frac{x^2}{4}+C.$

b) $\int x\sin xdx$;

Đặt $\{\begin{array}{c}u=x\\ dv=\sin xdx\end{array}\Rightarrow \{\begin{array}{c}du=dx\\ v=-c\mathrm{osx}\end{array}$

Khi đó:

$\begin{array}{c}\int x\sin xdx=-x.c\mathrm{osx}\mathrm{ }+\int \mathrm{cosxdx}=\mathrm{ }-x.c\mathrm{osx}\mathrm{ }+\mathrm{sinx}\mathrm{ }+\mathrm{ }\mathrm{C}\end{array}$

c) $\int (5-x).e^{x}dx$

Đặt $\{\begin{array}{c}u=5-x\\ dv=e^{x}dx\end{array}\Rightarrow \{\begin{array}{c}du=\mathrm{ }-dx\\ v=e^x\end{array}$

Khi đó:

$\int (5-x).e^{x}dx=(5-x).e^x-\int -e^{x}dx$

$=(5-x).e^x+{\int e}^x𝑑x$

$=(5-x).e^x+e^x+C.$

3. Khái niệm tích phân

3.1 Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

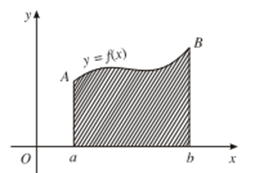
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a;  x = b (a < b); trục hoành và đường cong y = f(x),  trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in [a;b]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

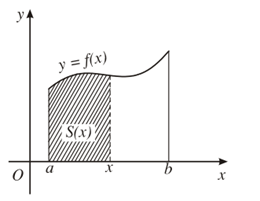
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) +  C.

Vì S(a) = 0 nên F(a) +  C = 0  hay C =  –  F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

3.2 Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)𝑑x.$

Ta còn dùng kí hiệu ${F\left(x\right)|}_a^b$