Trong các số phức có bao nhiêu số thuần ảo?
A. 4
B. 1
C. 3
D. 2
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Có 2 số thuần ảo, đó là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi A, B lần lượt là điểm biểu diễn cho hai số phức và . Gọi M là trung điểm của AB. Khi đó M là điểm biểu diễn cho số phức nào dưới đây?
Gọi A là điểm biểu diễn số phức và B là điểm biểu diễn của số phức . Mệnh đề nào sau đây là đúng?
Trong mặt phẳng tọa độ Oxy cho các điểm A, B như hình vẽ bên:
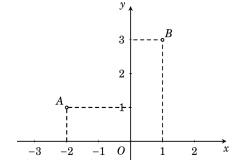
Trung điểm của đoạn thẳng AB biểu diễn số phức
Giả sử M, N, P, Q được cho ở hình bên là điểm biểu diễn của các số phức trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
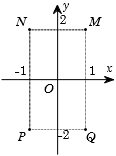
1. Số i.
Số i là số thỏa mãn: i2 = –1.
2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi , trong đó R; i2 = –1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.
Tập hợp các số phức kí hiệu là .
Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; .
Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.
– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :
a + bi = c + di a = c và b = d.
Ví dụ 3. Tìm các số thực x và y biết :
(2x – 1) + (y – 2)i = 3 + (4 – y)i
Lời giải:
Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i
Vậy x = 2 và y = 3.
– Chú ý :
a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có : .
b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi
Đặc biệt : i = 0 + 1.i
Số i được gọi là đơn vị ảo.
Ví dụ 4. Số phức z có phần thực là và phần ảo là là .
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.
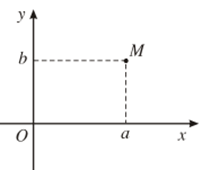
Ví dụ 5.
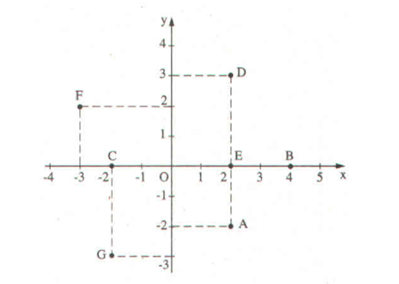
Điểm A biểu diễn số phức 2 – 2i
Điểm B biểu diễn số phức 4.
Điểm C biểu diễn số phức – 2.
Điểm D biểu diễn số phức 2 + 3i.
Điểm E biểu diễn số phức 2.
Điểm F biểu diễn số phức – 3 + 2i.
Điểm G biểu diễn số phức –2 – 3i.
5. Mô đun của số phức.
Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.
Độ dài của vecto được gọi là môđun của số phức z và kí hiệu là |z|.
Vậy hay .
Ta thấy :.
Ví dụ 6.
6. Số phức liên hợp
– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là
Ví dụ 7.
Nếu z = – 3 + 5i thì
Nếu z = – 4 + 4i thì
– Nhận xét :
+ Trên mặt phẳng tọa độ các điểm biểu diễn z và đối xứng nhau qua trục Ox.
+ Từ định nghĩa ta có: