Trong mặt phẳng, hình nào sau đây có trục đối xứng?

I. Định nghĩa.

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

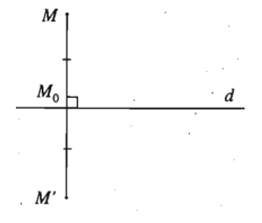
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đd.

- Nếu hình ℋ ' là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ' qua d, hay ℋ  và ℋ ' đối xứng với nhau qua d.

- Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi $M_0$ là hình chiếu vuông góc của M trên đường thẳng d. Khi đó: M’ = Đd(M) $\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}$.

2) M’ = Đd(M) $\iff$M = Đd(M’).

II. Biểu thức tọa độ.

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’ ; y’) thì $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’; y’) thì $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ 1. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi ĐOx(M) = A(x ; y) và ĐOy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

$\left\{\begin{array}{c}x=2\\ y=-4\end{array}\Rightarrow A(2;-4)\right.$

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

$\left\{\begin{array}{c}a=-2\\ b=4\end{array}\Rightarrow B(-2;4)\right.$

III. Tính chất.

- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

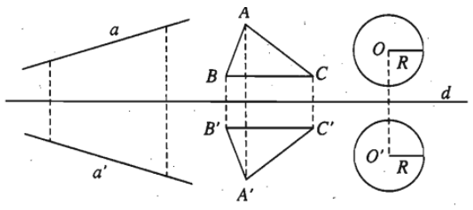
Ví dụ 2. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)^2 + (y – 3)^2 = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)^2 + (y + 3)^2 = 36.

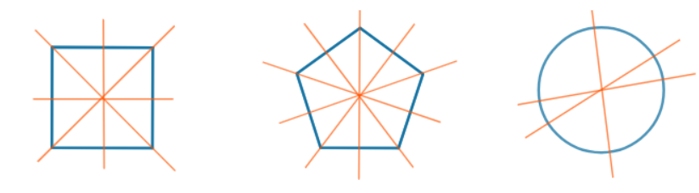
IV. Trục đối xứng của một hình

- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

- Ví dụ 3. Các hình sau có trục đối xứng