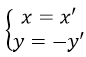Trắc nghiệm Toán 11 Bài 3: Phép đối xứng trục (phần 1) (có đáp án)
-
803 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
 Xem đáp án
Xem đáp án
Tìm ảnh của từng điểm qua phép đối xứng trục AC:
Suy ra, qua phép đối xứng trục AC, biến tam giác IBG thành tam giác IDH.
Chọn đáp án C
Câu 2:
Trong mặt phẳng Oxy cho điểm M(-1;3). Phép đối xứng trục Ox biến M thành M’ thì tọa độ M’ là:
 Xem đáp án
Xem đáp án
Áp dụng biểu thức tọa độ của phép đối xứng trục Ox , ta có:
Chọn đáp án C
Câu 3:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
 Xem đáp án
Xem đáp án
Xét phép đối xứng trục Ox, biến đường thẳng d thành đường thẳng d'.
Biến mỗi điểm M(x, y)d thành điểm M'(x'; y')d'
Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có
Vì M (x; y) nằm trên đường thẳng d nên: x - 2y + 4 = 0
thay vào ta được x'+ 2y' + 4 = 0
Suy ra, phương trình đường thẳng d' là : x + 2y + 4 = 0.
Chọn đáp án B
Câu 4:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: . Phép đối xứng trục Oy biến (C) thành (C’) có phương trình
 Xem đáp án
Xem đáp án
Đường tròn (C) có tâm : I( 3; 1) và bán kính:
Phép đối xứng trục Oy, biến đường tròn (C) thành đường tròn (C'), biến tâm I thành tâm I' và bán kính R' = R
+ Tìm tọa độ điểm I'.
Áp dụng biểu thức tọa độ của đối xứng trục Oy ta được:
Phương trình đường tròn (C') là :
Chọn đáp án B.
Câu 5:
Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
 Xem đáp án
Xem đáp án
Đáp án D
Phép đối xứng trục Oy có:
Suy ra
Vậy ảnh của điểm (2; 3) qua phép đối xứng trục Oy là D(-2; 3).
Đáp án D
Câu 6:
Trong các mệnh đề sau mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Phương án A. Tam giác đều chỉ có ba trục đối xứng là ba đường cao.
Phương án B. Đường thẳng cũng có vô số trục đối xứng (là đường thẳng bất kì vuông góc với đường thẳng đã cho).
Phương án C. Hình gồm hai đường thẳng vuông góc có bốn trục đối xứng (là chính hai đường thẳng đó và hai đường phân giác của góc tạo bởi hai đường thẳng đó).
Phương án D: Hình tròn có vô số trục đối xứng. Trục đối xứng là 1 đường thẳng bất kì đi qua tâm đường tròn.
Đáp án D
Câu 7:
Trong mặt phẳng, hình vuông có mấy trục đối xứng?
 Xem đáp án
Xem đáp án
Hình vuông có 4 trục đối xứng bao gồm:
Hai đường chéo và hai đường trung bình.
Đáp án D
Câu 8:
Trong mặt phẳng, hình nào sau đây có trục đối xứng?
 Xem đáp án
Xem đáp án
Tam giác cân có trục đối xứng là đường cao (cũng là trung trực, phân giác).
Đáp án D
Câu 9:
Trong mặt phẳng, cho hình thang cân ABCD có hay đáy là AB và CD. Tìm mệnh đề đúng:
 Xem đáp án
Xem đáp án
Đáp án D
Gọi E, F lần lượt là trung điểm của AB và CD
Khi đó B đối xứng với A qua EF và C đối xứng với D qua EF
Vậy ta có phép đối xứng với trục biến DA thành CB nên DA = CB
Câu 10:
Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc . Có bao nhiêu phép đối xứng trục biến a thành b.
 Xem đáp án
Xem đáp án
Có hai phép đối xứng trục biến đường thẳng a thành đường thẳng b
Trục đối xứng là : hai đường phân giác của góc tạo bởi a và b.
Nhận xét: Giả thiết góc chỉ để gây nhiễu
Đáp án B
Câu 11:
Có bao nhiêu phép đối xứng trục biến một hình chữ nhật thành chính nó?
 Xem đáp án
Xem đáp án
Có hai phép đối xứng trục biến một hình chữ nhật thành chính nó.
Trục đối xứng là hai đường thẳng đi qua tâm hình chữ nhật và vuông góc với hai cặp cạnh đối diện của nó.
Đáp án C
Câu 12:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình
 Xem đáp án
Xem đáp án
Phép đối xứng trục Oy : biến đường thẳng d thành đường thẳng d'.
Biến mỗi điểm M (x, y) thuộc d thành điểm M'(x'; y') thuộc d'.
Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:
Vì điểm M(x y) thuộc đường thẳng d nên: x + y - 2 = 0
suy ra: - x'+ y'- 2 = 0 hay x ' - y' + 2 = 0
Do đó, phương trình đường thẳng d' là : x - y +2 = 0
Đáp án B
Câu 13:
Trong mặt phẳng Oxy cho parabol (P) có phương trình: . Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
 Xem đáp án
Xem đáp án
Phép đối xứng trục Ox, biến parabol (P) thành parabol (P')
và biến mỗi điểm M(x, y) thuộc (P) thành điểm M'(x'; y') thuộc (P')
Áp dụng biểu thức tọa đọ của phép đối xứng trục Ox ta có:
Vì điểm M thuộc (P) nên :
suy ra:
Suy ra, phương trình (P') là :
Thay vào phương trình (P) ta được: hay
Đáp án C
Câu 14:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: . Phép đối xứng trục Oy biến (C) thành (C’) có phương trình:
 Xem đáp án
Xem đáp án
Phép đối xứng qua trục Oy biến đường tròn (C) thành đường tròn (C')
Biến mỗi điểm M(x, y) thuộc (C) thành điểm M'(x'; y') thuộc (C')
Áp dụng biểu thức tọa độ của phép đối xứng qua trục Oy ta được:
Vì điểm M thuộc (C) nên:
Suy ra:
Suy ra, phương trình đường tròn (C') là
Đáp án B
Câu 15:
Trên tia phân giác ngoài Cx của góc C của tam giác ABC lấy điểm M không trùng với C. tìm mệnh đề đúng nhất:
 Xem đáp án
Xem đáp án
Lấy A’ đối xứng A qua Cx.
Suy ra: MA = MA' và CA = CA'
Ta có:
MA + MB = MA’ + MB > BA’ = CB + CA’ = CB + CA
Nhận xét: Bất đẳng thức tam giác: Trong một tam giác bất kì luôn có tổng hai cạnh lớn hơn cạnh thứ ba (chú ý giả thiết : M không trùng với C).
Đáp án B
Câu 16:
Trong mặt phẳng Oxy cho parabol (P) có phương trình . Phép đối xứng trục Oy biến (P) thành (P’) có phương trình:
 Xem đáp án
Xem đáp án
Phép đối xứng trục Oy, biến parabol (P) thành parabol (P')
Biến mỗi điểm M(x, y) thuộc (P) thành điểm M'(x '; y') thuộc (P')
Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta được:
Vì điểm M(x; y) thuộc (P) nên :
Suy ra:
Do đó, phương trình (P') là:
Đáp án B
Câu 17:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 8y + 11 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình:
 Xem đáp án
Xem đáp án
Phép đối xứng trục Oy, biến đường thẳng d thành đường thẳng d'
và biến mỗi điểm M(x , y) thuộc d thành điểm M' (x';y' ) thuộc d'
Áp dụng biểu thức tọa độ của phép đối xứng qua trục Oy ta có:
Vì điểm M(x, y) thuộc đường thẳng d nên: 2x - 8y +11 = 0
Suy ra: -2x' - 8y' + 11 = 0 hay 2x' + 8y ' - 11 = 0
Do đó, phương trình đường thẳng d' là : 2x + 8y -11 = 0
Đáp án A
Câu 18:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x-2y+2=0 và đường thằng l có phương trình : x - y + 1 = 0. Phép đối xứng trục l biến d thành d’ có phương trình
 Xem đáp án
Xem đáp án
Gọi giao điểm của d và l là điểm I. Tọa độ điểm I là nghiệm hệ:
Lấy A(4; 3) thuộc d. Phương trình đường thẳng a qua A và vuông góc với đường thẳng l có vecto chỉ phương là: nên có vecto pháp tuyến là:
Phương trình đường thẳng a: 1( x – 4) + 1.(y – 3) =0 hay x + y – 7 = 0
Gọi H là giao điểm của a và l.Tọa độ H là nghiệm hệ:
Gọi A’ là điểm đối xứng với A qua H. Khi đó, H là trung điểm của AA’.
Suy ra:
Phương trình đường thẳng IA’: đi qua I(0; 1) và có vecto chỉ phương . Phương trình IA’:
2( x- 0) - 1(y – 1) = 0 hay 2x – y + 1 = 0 chính là phương trình đường thẳng d’ đối xứng với d qua l.
Đáp án B
Câu 19:
Cho hai điểm A, B cùng phía với đường thẳng d. Gọi A’, B’ lần lượt là hình chiếu của A, B trên đường thẳng d. Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.
 Xem đáp án
Xem đáp án
Lấy A’’ đối xứng với A qua d.
Suy ra: CA = CA"
Chu vi tam giác ABC = AB + AC + BC = AB + CA’’+ CB
Vì độ dài AB không đổi nên để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB nhỏ nhất.
Lại có;
Do đó, để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB = A”B. Khi đó: B, C, A’’ thẳng hàng.
Vậy điểm C cần tìm là giao điểm của 2 đường thẳng A"B và d trong đó A" là điểm đối xứng với A qua d.
Đáp án D