Các số theo thứ tự đó lập thành một cấp số cộng, đồng thời, các số theo thứ tự đó lập thành một cấp số nhân. Hãy tìm x và y.
A. hoặc
B. hoặc
C. hoặc
D. hoặc
 Giải bởi Vietjack
Giải bởi Vietjack
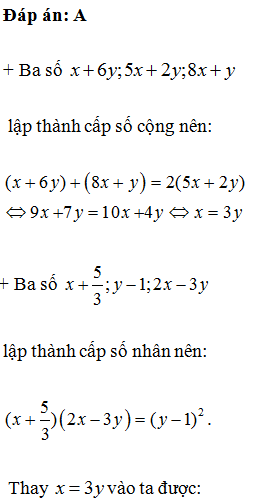
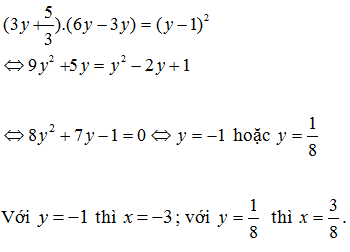
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân:
Tìm x để các số 2;8;x;128 theo thứ tự đó lập thành một cấp số nhân.
Cho các số 5x – y ; 2x + 3y ; x + 2y lập thành cấp số cộng ; các số lập thành cấp số nhân.Tính x, y
Tìm a, b biết rằng: 1, a, b là 3 số hạng liên tiếp của cấp số cộng và là 3 số hạng liên tiếp của một cấp số nhân.
Cho cấp số nhân thỏa mãn
Trên khoảng có bao nhiêu số hạng của cấp số.
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: ![]()
Số đo bốn góc của một tứ giác lồi lập thành một cấp số nhân, biết rằng số đo của góc lớn nhất gấp 8 lần số đo của góc nhỏ nhất. Tìm góc lớn nhất:
Cho hai số x và y biết các số theo thứ tự lập thành cấp số cộng và các số theo thứ tự đó lập thành cấp số nhân. Tìm x;y:
Aladin nhặt được cây đèn thần, chàng miết tay vào cây đèn và gọi Thần đèn ra. Thần đèn cho chàng 3 điều ước. Aladin ước 2 điều đầu tiên tùy thích, nhưng điều ước thứ 3 của chàng là: “Ước gì ngày mai tôi lại nhặt được cây đèn, và Thần cho tôi số điều ước gấp đôi số điều ước ngày hôm nay”. Thần đèn chấp thuận, và mỗi ngày Aladin đều thực hiện theo quy tắc như trên: ước hết các điều đầu tiên và luôn chừa lại điều ước cuối cùng để kéo dài thỏa thuận với thần Đèn cho ngày hôm sau. Hỏi sau 10 ngày gặp Thần đèn, Aladin ước tất cả bao nhiêu điều ước?
Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối hộp là và diện tích toàn phần là . Tính tổng số đo ba kích thước của hình hộp chữ nhật đó.
Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5;x;y;320 theo thứ tự đó lập thành cấp số nhận. Khẳng định nào sau đây là đúng?
Cho cấp số nhân có các số hạng lần lượt là . Tính tổng S của tất cả các số hạng của cấp số nhân đã cho
Biết rằng tồn tại hai giá trị và để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức
I. Định nghĩa
- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un + 1 = un. q với .
- Đặc biệt
Khi q = 0, cấp số nhân có dạng u1, 0, 0, …., 0,…..
Khi q = 1, cấp số nhân có dạng u1, u1, u1, …., u1,…
Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..
- Ví dụ 1. Dãy số hữu hạn sau là một cấp số nhân: 2, 4, 8, 16, 32 với số hạng đầu u1 = 2 và công bội q = 2.
II. Số hạng tổng quát.
- Định lí: Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức: un = u1.qn - 1 với n ≥ 2.
- Ví dụ 2. Cho cấp số nhân (un) với u1 = – 1; q = – 2.
a) Tính u6;
b) Hỏi 128 là số hạng thứ mấy.
Lời giải:
a) Ta có: u6 = u1. q5 = –1. (– 2)5 = 32.
b) Ta có: un = u1.qn - 1 nên 128 = – 1. (– 2)n - 1
(– 2)^n - 1 = – 128 = (– 2)7.
n – 1 = 7 nên n = 8.
Vậy 128 là số hạng thứ 8.
III. Tính chất các số hạng của cấp số nhân
- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:
( hay ).
IV. Tổng n số hạng đầu của một cấp số nhân.
- Định lí: Cho cấp số nhân (un) với công bội q ≠ 1. Đặt Sn = u1 + u2 + …+ un .
Khi đó: .
- Chú ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1,….u1,….Khi đó, Sn = n.u1.
Ví dụ 3. Cho cấp số nhân (un) biết u1 = 3; u2 = 9. Tính tổng của 8 số hạng đầu tiên?
Lời giải:
Ta có: u2 = u1.q nên 9 = 3q.
Suy ra, công bội q = 3.
Khi đó, tổng của 8 số hạng đầu tiên là:
.