Tất cả các giá trị của tham số m để phương trình có nghiệm là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
Đặt ta được
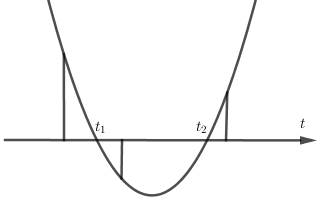
Phương trình (2) luôn có hai nghiệm ⇒ phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có ít nhất một nghiệm t sao cho , hay ít nhất một trong hai số 2; −2 phải nằm giữa hai nghiệm hay
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả các giá trị thực của m để phương trình có nghiệm thuộc đoạn :
Có bao nhiêu giá trị nguyên của m để phương trình có 4 nghiệm phân biệt
Để phương trình sau có 4 nghiệm phân biệt: . Giá trị của tham số a là:
Biết phương trình có một nghiệm có dạng , trong đó a, b, c là các số nguyên tố. Tính S=a+b+c
Một số tự nhiên có hai chữ số có dạng , biết hiệu của hai chữ số đó bằng 3. Nếu viết các chữ số theo thứ tự ngược lại thì được một số bằng số ban đầu trừ đi 10. Khi đó bằng
Tìm m để phương trình có hai nghiệm là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 là
Cho hàm số , có đồ thị (P). giả sử d là đường thẳng đi qua A(0; -3) và có hệ số góc k. Xác định k sao cho d cắt đồ thị (P) tại 2 điểm phân biệt, E, F sao cho vuông tại O (O là gốc tọa độ) . Khi đó
Hỏi có bao nhiêu giá trị m nguyên trong đoạn [0; 2017] để phương trình có hai nghiệm phân biệt?
Tập tất cả các giá trị của tham số m để phương trình có hai nghiệm dương phân biệt là:
Cho phương trình . Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm thỏa mãn . Khi đó tổng bình phương các giá trị tìm được của tham số m bằng: