Cho các số thực x,y thỏa mãn 4x2+4y2−2x2+4y2+1=23−x2−4y2−42−x2−4y2 . Gọi m,M lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P=x−2y+1x+y+4 . Tổng M+mbằng:
A.717
B.13
C.12
D.17
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
- Đặt ẩn phụ t=2x2+4y2(t≥1), đưa phương trình về dạng tích, giải phương trình tìm t.
- Tìm mối quan hệ giữa x,y dạng (ax)2+(by)2=1.
- Đặt {ax=sinαby=cosα, thế vào biểu thức P.
- Quy đồng, đưa biểu thức về dạng Asinα+Bcosα=C. Tìm điều kiện để phương trình có nghiệm, từ đó xác định M,m.
Giải chi tiết:
Ta có:
4x2+4y2−2x2+4y2+1=23−x2−4y2−42−x2−4y2
⇔(2x2+4y2)2−2.2x2+4y2=82x2+4y2−16(2x2+4y2)2
Đặt t=2x2+4y2(t≥1), phương trình trở thành:
t2−2t=8t−16t2⇔t2−2t=8t−16t2
⇒t3(t−2)=8(t−2)
⇒(t3−8)(t−2)=0
⇔(t−2)2(t2+2t+4)=0⇔t=2(tm)(dot2+2t+4>0∀t)
Với 2x2+4y2=2⇔x2+4y2=1. Khi đó tồn tại α sao cho {x=sinα2y=cosα.
Ta có:
P=x−2y−1x+y+4=sinα−cosα−1sinα+12cosα+4
⇔Psinα+12Pcosα+4P=sinα−cosα−1
⇔(P−1)sinα+(12P+1)cosα=−1−4P(*)
Để P tồn tại giá trị lớn nhất và giá trị nhỏ nhất thì phương trình (*) phải có nghiệm
⇒(P−1)2+(12P+1)2≥(−1−4P)2
⇔P2−2P+1+14P2+P+1≥16P2+8P+1
⇔594P2+9P−1≤0⇔−18−4√3559≤P≤−18+4√3559
⇒{M=−18+4√3559m=−18−4√3559⇒M+m=−3659
Đáp án A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu số tự nhiên có 4 chữ số khác nhau và khác 0 mà trong mỗi số luôn có mặt hai chữ số chẵn là hai chữ số lẻ?
Gieo một con súc sắc cân đối và đồng chất hai lần. Tính xác suất để ít nhất một lần xuất hiện mặt sáu chấm.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD=a,AB=2a . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng (AMN) .
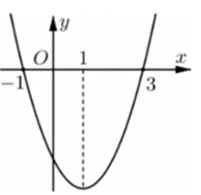
Cho hàm số y=f(x) có đồ thị f' là parabol như hình vẽ bên. Khẳng định nào sau đây là đúng?
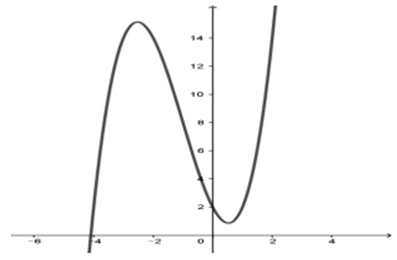
Cho hàm số bậc ba có đồ thị là đường cong như hình vẽ bên. Hỏi phương trình có bao nhiêu nghiệm phân biệt.
Tính tổng các giá trị nguyên của tham số m trên để hàm số nghịch biến trên khoảng .
Cho hình lăng trụ có đáy là tam giác vuông cân tại B và . Hình chiếu vuông góc của trên mặt phẳng là trung điểm H của cạnh AB và . Thể tích của khối lăng trụ đã cho bằng: