Cho hình lập phương ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình vuông A'B'C'D' và M là điểm thuộc đoạn thẳng OI sao cho MO=2MI. Khi đó côsin của góc tạo bởi hai mặt phẳng (MC'D') và (MAB) bằng:
A.
B.
C.\[\frac{{7\sqrt {85} }}{{85}}\]
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
- Sử dụng định lí: Góc giữa hai mặt phẳng là giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Xác định góc giữa hai mặt phẳng, sử dụng định lí Pytago và định lí Côsin trong tam giác để tính góc.
Giải chi tiết:
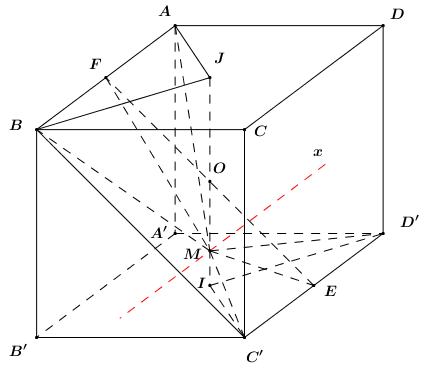
Gọi E,F lần lượt là trung điểm của C'D',AB.
Xét và có MI chung, Ic'=Id' nên (2 cạnh góc vuông)
cân tại E .
Chứng minh tương tự ta có .
Xét (MC'D') và (MAB) có M chung,
.
Lại có .
Ta có: \[\left\{ {\begin{array}{*{20}{l}}{\left( {MC'D'} \right) \cap \left( {MAB} \right) = Mx}\\{ME \subset \left( {MC'D'} \right),{\mkern 1mu} {\mkern 1mu} ME \bot Mx}\\{MF \subset \left( {MAB} \right),{\mkern 1mu} {\mkern 1mu} MF \bot Mx}\end{array}} \right.\]
.
Giả sử ABCD.A'B'C'D' là khối lập phương có cạnh bằng 1.
Ta có .
Áp dụng định lí Pytago ta có:
Tương tự ta có
Dễ thấy BC'EF là hình bình hành nên .
Áp dụng định lí Côsin trong tam giác MEF ta có:
Mà góc giữa hai mặt phẳng là góc nhọn, có giá trị côsin là số dương.
Vậy .
Đáp án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tập hợp tất cả các giá trị của tham số m để hàm số có tập xác định là \[\mathbb{R}\].
Tìm tất cả các giá trị của tham số m để đồ thị hàm số có tiệm cận đứng.
Cho giới hạn , với \[\frac{a}{b}\] là phân số tối giản. Tính giá trị của biểu thức .
Trên giá sách có 6 quyển sách Toán khác nhau, 7 quyển sách Văn khác nhau và 8 quyển sách Tiếng Anh khác nhau. Có bao nhiêu cách lấy 2 quyển sách thuộc 2 môn khác nhau?
Cho đa giác lồi . Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Xác suất để 3 đỉnh được chọn tạo thành 1 tam giác không có cạnh nào là cạnh của đa giác đã cho bằng:
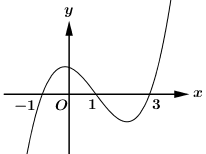
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết hàm số y=f'(x) có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên để hàm số nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử?
Gọi S là tập hợp tất cả các giá trị nguyên m để đồ thị hàm số có 7 điểm cực trị. Tính tổng các phần tử của S.
Cho hàm số , có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến Δ với đồ thị (C) tại A cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất.
Cho hình chóp \[S.ABCD\] có đáy là hình vuông tâm O, cạnh a, SO vuông góc với mặt phẳng \[\left( {ABCD} \right)\] và SO=a. Khoảng cách giữa SC và AB bằng:
Cho hình chóp S.ABC có AB=AC=4, BC=2, , . Gọi lần lượt là trọng tâm các tam giác và T đối xứng với S qua mặt phẳng (ABC). Thể tích khối chóp bằng \[\frac{a}{b}\], với và tối giản. Tính giá trị của biểu thức .
Cho hình chóp \[S.ABCD\] có đáy ABCD là hình vuông cạnh a, , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp SABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp hình chóp là:
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a. góc giữa cạnh bên và mặt đáy bằng Tính thể tích của khối nón có đỉnh là S và đáy là đường tròn ngoại tiếp