Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh bằng a không đổi. Độ dài CD thay đổi. Tính giá trị lớn nhất đạt được của thể tích khối tứ diện ABCD.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
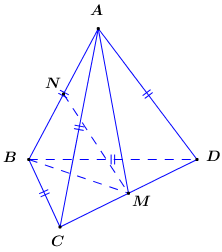
Gọi M, N lần lượt là trung điểm của CD, AB.
Vì tam giác ABC, ABD là các tam giác đều cạnh a nên AB = AC = AD = BC = BD = a.
là các tam giác cân tại A .
Lại có cân tại M .
.
Đặt CD = x ta có .
Do đó ta có
Để đạt giá trị lớn nhất thì
Áp dụng BĐT Cô-si ta có .
Dấu “=” xảy ra .
Vậy .
Đáp án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số . Tìm m để mọi bộ ba số phân biệt a, b, c thuộc đoạn thì là độ dài ba cạnh của một tam giác.
Tìm tất cả các điểm M nằm trên đồ thị hàm số mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng .
Một người gửi tiền vào ngân hàng với lãi suát không đổi là 6% trên năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (lãi kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút ra 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng (làm tròn đến hàng triệu) là bao nhiêu triệu đồng?
Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai đường kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng . Tính thể tích khối tứ diện ABCD.
Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh a, ACD và BCD là các tam giác vuông tương ứng tại A và B. Tính thể tích khối tứ diện ABCD.
Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm . Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.
Sau đây, có bao nhiêu hàm số mà đồ thị có đúng một tiệm cận ngang?
1) \[y = \frac{{\sin x}}{x}\] 2)
3) 4)
Cho hàm số có đạo hàm \[f'\left( x \right) = - \frac{x}{{{x^2} + 1}}\]. Với a và b là các số dương thỏa mãn , giá trị nhỏ nhất của hàm số trên đoạn bằng:
Cho tứ diện ABCD có ABC, ABD, ACD là các tam giác vuông tương ứng tại A, B, C. Góc giữa AD và (ABC) bằng , và khoảng cách giữa AD và BC bằng a. Tính thể tích khối tứ diện ABCD.