Cho tứ diện \(ABCD\) có \(AB = 2a,AC = 3a,AD = 4a,\widehat {BAC} = \widehat {CAD} = \widehat {DAB} = {60^0}.\) Thể tích khối tứ diện \(ABCD\) bằng
A.\(4\sqrt 2 {a^3}.\)
B.\(\sqrt 2 {a^3}.\)
C.\(3\sqrt 2 {a^3}.\)
D. \(2\sqrt 2 {a^3}.\)
Giải bởi Vietjack
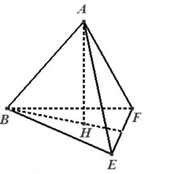
Trên các cạnh \(AC,AD\) lần lượt lấy các điểm \(E,F\) sao cho \(AE = AF = 2a \Rightarrow ABEF\) là tứ diện đều cạnh \(2a.\)
Gọi \(H\) là trọng tâm của \(\Delta BEF \Rightarrow BH = \frac{{2a\sqrt 3 }}{3} \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \frac{{2a\sqrt 6 }}{3}.\)
\( \Rightarrow {V_{ABEF}} = \frac{1}{3}AH.{S_{BEF}} = \frac{1}{3}.\frac{{2a\sqrt 6 }}{3}.{a^2}\sqrt 3 = \frac{{2\sqrt 2 {a^3}}}{3}.\)
Vì \(\frac{{{V_{ABCD}}}}{{{V_{ABEF}}}} = \frac{{AB}}{{AB}}.\frac{{AC}}{{AE}}.\frac{{AD}}{{AF}} = \frac{3}{2}.A = 3 \Rightarrow {V_{ABCD}} = 2\sqrt 2 {a^3}.\)
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm điều kiện của tham số \(b\) để hàm số \(y = {x^4} + b{x^2} + c\) có 3 điểm cực trị?
Với giá trị nào của \(m\) thì đồ thị hàm số \(y = \frac{{2{x^2} + 6mx + 4}}{{mx + 2}}\) đi qua điểm \(A\left( { - 1;4} \right)?\)
Đồ thị của hai hàm số \(y = 4{x^4} - 2{x^2} + 1\) và \(y = {x^2} + x + 1\) có tất cả bao nhiêu điểm chung?
Cho đồ thị \(\left( {{C_m}} \right):y = {x^3} - 2{x^2} + \left( {1 - m} \right)x + m.\) Khi thì \(\left( {{C_m}} \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 4.\) Khẳng định nào sau đây đúng?
Nếu \({a^{\frac{{13}}{{17}}}} >{a^{\frac{{15}}{{18}}}}\) và \({\log _b}\left( {\sqrt 2 + \sqrt 5 } \right) >{\log _b}\left( {2 + \sqrt 3 } \right)\) thì
Giả sử các biểu thức chứa logarit đều có nghĩa. Mệnh đề nào sau đây đúng?
Cho số thực dương \(a.\) Sauk hi rút gọn, biểu thức \(P = \sqrt[3]{{a\sqrt a }}\) có dạng
Cho \(a\) là số thực dương và \(m,n\) là các số thực tùy ý. Trong các tính chất sau, tính chất nào đúng?
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = m{x^4} + \left( {m - 3} \right){x^2} + 3m - 5\) chỉ có cực tiểu mà không có cực đại.
Cho đường cong \(\left( C \right)\) có phương trình \(y = \frac{{x - 1}}{{x + 1}}.\) Gọi \(M\) là giao điểm của \(\left( C \right)\) với trục tung. Tiếp tuyến của \(\left( C \right)\) tại \(M\) có phương trình là
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Trên các đoạn \(SA,SB,SC,SD\) lấy lần lượt các điểm \(E,F,G,H\) thỏa mãn \(\frac{{SE}}{{SA}} = \frac{{SG}}{{SC}} = \frac{1}{3},\frac{{SF}}{{SB}} = \frac{{SH}}{{SD}} = \frac{2}{3}.\) Tỉ số thể tích khối \[EFGH\] với khối \(S.ABCD\) bằng:
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{x - 3}}.\) Chọn mệnh đề sai trong các mệnh đề sau đây?
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B,SA\) vuông góc với đáy và \(SA = AB = 6a.\) Tính thể tích khối chóp \(S.ABC\).
