Cho các số thực \(x,y\) thỏa mãn \(x - 3\sqrt {x + 1} = 3\sqrt {y + 2} - y.\) Giá trị nhỏ nhất của biểu thức \(P = x + y\) là
A. \(\min P = - 63.\)
B.\(\min P = - 91.\)
C. \(\min P = 9 + 3\sqrt {15} .\)
Giải bởi Vietjack
Đáp án D.
Theo giả thiết: \(x - 3\sqrt {x + 1} = 3\sqrt {y + 2} - y\left( * \right).\)
Điều kiện: \(x \ge - 1,y \ge - 2.\)
Ta có: \(P = x + y \Leftrightarrow y = P - x,\) thế vào \(\left( * \right)\) ta được:
\(3\sqrt {x + 1} + 3\sqrt {P - x + 2} = P{\rm{ }}\left( 1 \right)\)
Ta đi tìm giá trị nhỏ nhất của \(P\) để phương trình \(\left( 1 \right)\) có nghiệm \(x \ge - 1.\)
\(\left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l}P \ge 0\\2\sqrt {\left( {x + 1} \right)\left( {P - x + 2} \right)} = \frac{{{P^2}}}{9} - P - 3\end{array} \right.\)
Để có nghiệm thì \(\frac{{{P^2}}}{9} - P - 3 \ge 0 \Leftrightarrow \left[ \begin{array}{l}P \ge \frac{{9 + 3\sqrt {21} }}{2}\\P \le \frac{{9 - 3\sqrt {21} }}{2}\end{array} \right. \Rightarrow P \ge \frac{{9 + 3\sqrt {21} }}{2}.\)
Với giá trị nhỏ nhất \(P = \frac{{9 + 3\sqrt {21} }}{2}\) thì phương trình \(\left( 1 \right)\) có nghiệm \(x = - 1,\) suy ra:
\( \Rightarrow y = P - x = \frac{{9 + 3\sqrt {21} }}{2} + 1 = \frac{{11 + 3\sqrt {21} }}{2}.\)
Mặt khác, ta lại có:\(P = x + y \Leftrightarrow x = P - y,\) thế vào (*) ta được:
\(P = 3\sqrt {P - y + 1} + 3\sqrt {y + 2} \) \(\left( 2 \right)\)
Ta đi tìm giá trị nhỏ nhất của \(P\) để phương trình \(\left( 2 \right)\) có nghiệm \(y \ge - 2.\)
\(\left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l}P \ge 0\\2\sqrt {\left( {y + 2} \right)\left( {P - y + 1} \right)} = \frac{{{P^2}}}{9} - P - 3\end{array} \right.\)
Để có nghiệm thì \(\frac{{{P^2}}}{9} - P - 3 \ge 0 \Leftrightarrow \left[ \begin{array}{l}P \ge \frac{{9 + 3\sqrt {21} }}{2}\\P \le \frac{{9 - 3\sqrt {21} }}{2}\end{array} \right. \Rightarrow P \ge \frac{{9 + 3\sqrt {21} }}{2}.\)
Với giá trị nhỏ nhất \(P = \frac{{9 + 3\sqrt {21} }}{2}\) thì phương trình \(\left( 2 \right)\) có nghiệm \(y = - 2,\) suy ra:
\( \Rightarrow x = P - y = \frac{{9 + 3\sqrt {21} }}{2} + 2 = \frac{{13 + 3\sqrt {21} }}{2}.\)
Vậy \({P_{\min }} = \frac{{9 + 3\sqrt {21} }}{2} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = - 1\\y = \frac{{11 + 3\sqrt {21} }}{2}\end{array} \right.\\\left\{ \begin{array}{l}x = \frac{{13 + 3\sqrt {21} }}{2}\\y = - 2\end{array} \right.\end{array} \right.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu giá trị nguyên của tham số \(m \in \left( {0;20} \right]\) để hàm số \(y = \frac{{x + 2}}{{x + 3m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 6} \right)?\)
Đồ thị của hàm số \[y = {x^3} - 3{x^2} - 9x + 1\] có hai điểm cực trị là \(A\) và \(B.\) Điểm nào dưới đây thuộc đường thẳng \(AB?\)
Gọi \(S\) là tập hợp các số tự nhiên có 6 chữ số được lập từ tập hợp \(A = \left\{ {0;1;2;...;9} \right\}.\) Chọn ngẫu nhiên một số từ tập \(S.\) Tính xác suất để chọn được số tự nhiên có tích các chữ số là 1400.
Gọi \(m\) là tham số thực để giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m - 4} \right|\) trên đoạn \(\left[ { - 2;1} \right]\) đạt giá trị nhỏ nhất. Giá trị của \(m\) là
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left| {\sin x - \cos x} \right| + 4\sin 2x = m\) có nghiệm thực?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
![Cho hàm số y=f(x) có bảng biến thiên như sau: Biết f(0) = 0, số nghiệm thuộc đoạn [-pi/6;7pi/6] của phương trình (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid0-1651912716.png)
Biết \(f\left( 0 \right) = 0,\) số nghiệm thuộc đoạn \(\left[ { - \frac{\pi }{6};\frac{{7\pi }}{3}} \right]\) của phương trình \(f\left( {f\left( {\sqrt 3 \sin x + \cos x} \right)} \right) = 1\) là
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 3} \right)^{2020}}\left( {{\pi ^{2x}} - {\pi ^x} + 2021} \right)\left( {{x^2} - 2x} \right),\forall x \in \mathbb{R}.\) Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {{x^2} - 8x + m} \right)\) có đúng ba điểm cực trị \({x_1},{x_2},{x_3}\) thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 50.\) Khi đó tổng các phần tử của \(S\) bằng
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 1}}{{1 - x}}\) là
Cho hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - m - 1} \right)x + 1.\) Có bao nhiêu giá trị nguyên của tham số thực \(m\) để hàm số đạt cực trị tại \({x_1},{x_2}\) thỏa mãn \(x_1^2 + 2m{x_2} - 3{m^2} + m - 5 \le 0?\)
Từ các chữ số 1, 2, 3, 4 lập được bao nhiêu số tự nhiên có 3 chữ số?
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau
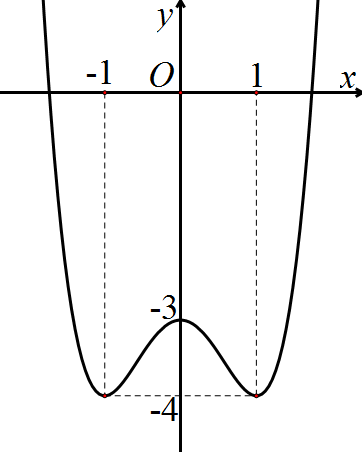
Tất cả các giá trị của tham số thực \(m\) để phương trình \(f\left( x \right) = m\) có 4 nghiệm phân biệt là
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 8.\) Công bội của cấp số nhân đã cho bằng
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
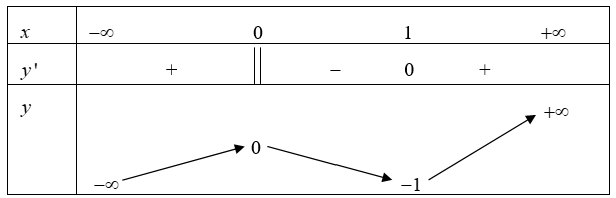
Khẳng định nào sau đây là khẳng định đúng?
