Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng \(2500\) năm trước Công nguyên. Kim tự tháp này có hình dạng là một khối chóp tứ giác đều có chiều cao \(147\) m, cạnh đáy dài \(230\) m. Thể tích \(V\) của khối chóp đó là
A. \(V = 2592100\)m3
B. \(V = 7776300\)m3
C. \(V = 2592300\)m3
D. \(V = 3888150\)m3
 Giải bởi Vietjack
Giải bởi Vietjack
Áp dụng công thức, ta có: \(V = \frac{1}{3}B.h = \frac{1}{3}{230^2}.147 = 2592100{m^3}.\)
Đáp án A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \[f\left( x \right) = {x^3} - 3x + m\] ( với m là tham số thực). Biết \[\mathop {\max }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = 5\] . Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left( {0; + \infty } \right)\)là
Hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + dx + e\) có đồ thị như hình dưới đây. Số nghiệm của phương trình \(f\left( {f\left( x \right)} \right) + 1 = 0\) là
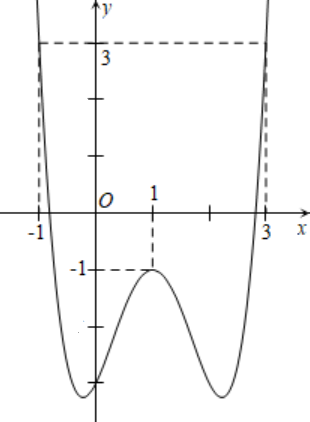
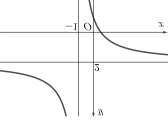
Đường cong ở hình vẽ dưới đây là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực .
Mệnh đề nào dưới đây đúng?
Có bao nhiêu giá trị nguyên dương của tham số \(m\) không vượt quá 2020 để hàm số \(y = - {x^4} + (m - 5){x^2} + 3m - 1\) có ba điểm cực trị
Cho hàm số \(f\left( x \right) = a{x^5} + b{x^3} + cx;(a > 0;b > 0)\) thỏa mãn \(f\left( 3 \right) = - \frac{7}{3};f\left( 9 \right) = 81\). Gọi \[S\] là tập hợp tất cả các giá trị của tham số \[m\] sao cho \[\mathop {\max }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| + \mathop {\min }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| = 86\] với \(g\left( x \right) = f\left( {1 - 2x} \right) + 2.f\left( {x + 4} \right) + m\). Tổng của tất cả các phần tử của \[S\] bằng
Cho hàm số\(y = {x^3} + (m - 1){x^2} - 3mx + 2m + 1\) có đồ thị , biết rằng đồ thị\(({C_m})\) luôn đi qua hai điểm cố định\(A,\,B.\) Có bao nhiêu số nguyên dương \(m\)thuộc đoạn \(\left[ { - 2020;2020} \right]\) để \(({C_m})\) có tiếp tuyến vuông góc với đường thẳng \(AB\)?
Cho hàm số \[y = \frac{{x + 1}}{{{x^2} - 2x - 3}}\]. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Mặt phẳng \[(AB'C')\] chia khối lăng trụ \[ABC.A'B'C'\] thành hai khối đa diện \[AA'B'C'\] và \[ABCC'B'\]có thể tích lần lượt là \[{V_1},\,{V_2}\]. Khẳng định nào sau đây đúng?
Kết quả \(\mathop {\lim }\limits_{x \to - 1} \frac{{x + 1}}{{2{x^3} + 2}}\) bằng:
Cho đa giác đều có 10 cạnh. Số tam giác có 3 đỉnh là ba đỉnh của đa giác đều đã cho là
Ông A dự định sử dụng hết \(8{\rm{ }}{m^2}\)kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng ( các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (làm tròn đến hàng phần trăm)?
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = (x + 1){(x - 2)^3}{(x - 3)^4}{(x + 5)^5}{\rm{; }}\forall x \in \mathbb{R}\) . Hỏi hàm số \(y = f(x)\) có mấy điểm cực trị?
Có bao nhiêu giá trị của tham số \(m\) để hàm số \(y = {x^3} + \frac{1}{2}({m^2} - 1){x^2} + 1 - m\) có điểm cực đại là \(x = - 1\)?
Tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{{x^2} - 2x - m}}\) có đúng hai tiệm cận đứng là