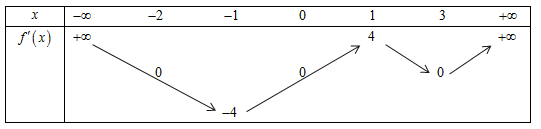
Cho hàm số \(f\left( x \right)\) có bảng biến thiên của hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Tính tổng các giá trị nguyên của tham số \(m \in \left( { - 10\,;\,10} \right)\) để hàm số \(y = f\left( {3x - 1} \right) + {x^3} - 3mx\) đồng biến trên khoảng \(\left( { - 2\,;\,1} \right)\)?
A. \( - 49\).
B. \( - 39\).
C. \( - 35\).
D. \(35\).
 Giải bởi Vietjack
Giải bởi Vietjack
Cách 1: Ta có: \(y' = 3f'\left( {3x - 1} \right) + 3{x^2} - 3m = 3\left( {f'\left( {3x - 1} \right) + {x^2} - m} \right)\)
Để hàm số đồng biến trên \(\left( { - 2;1} \right)\) thì:
\(y' \ge 0,\forall x \in \left( { - 2;1} \right) \Leftrightarrow \left( {f'\left( {3x - 1} \right) + {x^2} - m} \right) \ge 0,\forall x \in \left( { - 2;1} \right)\)
\(f'\left( {3x - 1} \right) + {x^2} \ge m,\forall x \in \left( { - 2;1} \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left( { - 2;1} \right)} \left( {f'\left( {3x - 1} \right) + {x^2}} \right)\)
Đặt \(f'\left( {3x - 1} \right) = g\left( x \right)\) và \({x^2} = h\left( x \right)\)
Quan sát bảng biến thiên ta có:
\(\left\{ \begin{array}{l}f'\left( {3x - 1} \right) \ge - 4 = f'\left( 0 \right),3x - 1 \in \left( { - 7;2} \right)\\h\left( x \right) = {x^2} \ge 0 = h\left( 0 \right),\forall x \in \left( { - 2;1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}f'\left( {3x - 1} \right) \ge - 4 = f'\left( 0 \right),\forall x \in \left( { - 2;1} \right)\\h\left( x \right) = {x^2} \ge 0 = h\left( 0 \right),\forall x \in \left( { - 2;1} \right)\end{array} \right.\)
\( \Rightarrow f'\left( {3x - 1} \right) + h\left( x \right) \ge - 4 + 0 = - 4,x = 0\)
\( \Rightarrow \mathop {\min }\limits_{\left( { - 2;1} \right)} \left[ {g\left( x \right) + h\left( x \right)} \right] = - 4,x = 0\)
Do đó: \(\mathop {\min }\limits_{\left( { - 2;1} \right)} \left( {f'\left( {3x - 1} \right) + {x^2}} \right) = - 4\)
Vì \(m \in \left( { - 10;10} \right)\) và \(m \le - 4\) nên tổng các giá trị nguyên của m thỏa mãn đề bài là -39
Cách 2:
Xét hàm số \(y = f\left( {3x - 1} \right) + {x^3} - 3mx\)
Ta có: \(y' = 3f'\left( {3x - 1} \right) + 3{x^2} - 3m = 3\left[ {f'\left( {3x - 1} \right) + {x^2} - m} \right]\)
Để hàm số đồng biến trên \(\left( { - 2;1} \right)\) thì:
\(y' \ge 0,\forall x \in \left( { - 2;1} \right) \Leftrightarrow f'\left( {3x - 1} \right) \ge - {x^2} + m,\forall x \in \left( { - 2;1} \right)\)
Đặt \(g\left( x \right) = f'\left( {3x - 1} \right) \ge - {x^2} + m = h\left( x \right),\forall x \in \left( { - 2;1} \right)\)
Đặt \(\left\{ \begin{array}{l}3x - 1 = t\\x = \frac{{t + 1}}{3}\\t \in \left( { - 7;2} \right)\end{array} \right. \Rightarrow f'\left( t \right) \ge h\left( t \right) = - \frac{{{t^2} + 2t + 1}}{9} + m,\forall t \in \left( { - 7;2} \right)\left( * \right)\)
Ta có đồ thị hàm số \(h\left( t \right) = - \frac{{{t^2} + 2t + 1}}{9} + m\) có đỉnh \(I\left( { - 1;m} \right).\)
Vậy \(\left( * \right)\) thỏa mãn khi đồ thị \(h\left( t \right) = - \frac{{{t^2} + 2t + 1}}{9} + m\) nằm dưới đồ thị \(y = f'\left( t \right).\)
Suy ra: \(m \le - 4.\)
Với giả thiết \(m \in \left( { - 10;10} \right),m \in \mathbb{Z} \Rightarrow m \in \left[ { - 9; - 4} \right] \Rightarrow \sum\limits_{m = - 9}^{ - 4} m = - 39.\)
Đáp án B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \[f\left( x \right) = {x^3} - 3x + m\] ( với m là tham số thực). Biết \[\mathop {\max }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = 5\] . Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left( {0; + \infty } \right)\)là
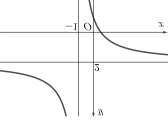
Hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + dx + e\) có đồ thị như hình dưới đây. Số nghiệm của phương trình \(f\left( {f\left( x \right)} \right) + 1 = 0\) là
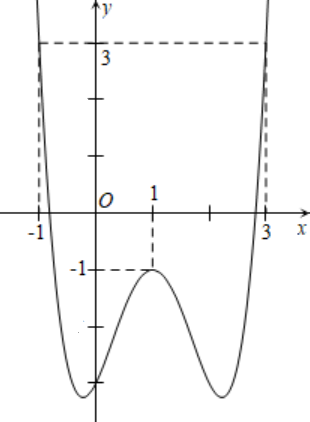
Đường cong ở hình vẽ dưới đây là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực .
Mệnh đề nào dưới đây đúng?
Có bao nhiêu giá trị nguyên dương của tham số \(m\) không vượt quá 2020 để hàm số \(y = - {x^4} + (m - 5){x^2} + 3m - 1\) có ba điểm cực trị
Cho hàm số \(f\left( x \right) = a{x^5} + b{x^3} + cx;(a > 0;b > 0)\) thỏa mãn \(f\left( 3 \right) = - \frac{7}{3};f\left( 9 \right) = 81\). Gọi \[S\] là tập hợp tất cả các giá trị của tham số \[m\] sao cho \[\mathop {\max }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| + \mathop {\min }\limits_{\left[ { - 1;5} \right]} \left| {g\left( x \right)} \right| = 86\] với \(g\left( x \right) = f\left( {1 - 2x} \right) + 2.f\left( {x + 4} \right) + m\). Tổng của tất cả các phần tử của \[S\] bằng
Cho hàm số\(y = {x^3} + (m - 1){x^2} - 3mx + 2m + 1\) có đồ thị , biết rằng đồ thị\(({C_m})\) luôn đi qua hai điểm cố định\(A,\,B.\) Có bao nhiêu số nguyên dương \(m\)thuộc đoạn \(\left[ { - 2020;2020} \right]\) để \(({C_m})\) có tiếp tuyến vuông góc với đường thẳng \(AB\)?
Cho hàm số \[y = \frac{{x + 1}}{{{x^2} - 2x - 3}}\]. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Mặt phẳng \[(AB'C')\] chia khối lăng trụ \[ABC.A'B'C'\] thành hai khối đa diện \[AA'B'C'\] và \[ABCC'B'\]có thể tích lần lượt là \[{V_1},\,{V_2}\]. Khẳng định nào sau đây đúng?
Kết quả \(\mathop {\lim }\limits_{x \to - 1} \frac{{x + 1}}{{2{x^3} + 2}}\) bằng:
Cho đa giác đều có 10 cạnh. Số tam giác có 3 đỉnh là ba đỉnh của đa giác đều đã cho là
Ông A dự định sử dụng hết \(8{\rm{ }}{m^2}\)kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng ( các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (làm tròn đến hàng phần trăm)?
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = (x + 1){(x - 2)^3}{(x - 3)^4}{(x + 5)^5}{\rm{; }}\forall x \in \mathbb{R}\) . Hỏi hàm số \(y = f(x)\) có mấy điểm cực trị?
Có bao nhiêu giá trị của tham số \(m\) để hàm số \(y = {x^3} + \frac{1}{2}({m^2} - 1){x^2} + 1 - m\) có điểm cực đại là \(x = - 1\)?
Tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{{x^2} - 2x - m}}\) có đúng hai tiệm cận đứng là