Cho dãy số {${\mathrm{u}}_{\mathrm{n}}$ } thỏa mãn $2^{4{\mathrm{u}}_1+1}+2^{3-2{\mathrm{u}}_2}=\frac{8}{{\log }_2(2{\mathrm{u}}_3^2-8{\mathrm{u}}_2+4)}$và  ${\mathrm{u}}_{\mathrm{n}+1}=2{\mathrm{u}}_{\mathrm{n}}$với mọi n∈N^*. Tìm giá trị nhỏ nhất của n để ${\mathrm{u}}_1+{\mathrm{u}}_2+.....+{\mathrm{u}}_{\mathrm{n}}<2^{2019}$.

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết SA⊥(ABC) và SA=a$\sqrt{3}$. Tính theo a thể tích của khối chóp S.ABC.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a$\sqrt{3}$ và vuông góc với đáy. Gọi G là trọng tâm tam giác BCD. Tính khoảng cách từ G đến mặt phẳng (SBC).

Cho tam giác ABC có BC=a,AC=b,AB=c và bán kính đường tròn ngoại tiếp tam giác ABC bằng R. Tìm khẳng đính sai trong các khẳng định sau?

Cho hàm số $\mathrm{y}=\frac{-\mathrm{mx}+3}{3\mathrm{x}-\mathrm{m}}$ với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S

Có bao nhiêu giá trị nguyên của tham số m∈[-10;10] để hàm số y=|2${\mathrm{x}}^4-2{\mathrm{x}}^3-{\mathrm{x}}^2+\mathrm{m}$| có 5 điểm cực trị 

Cho hai số phức z,w thỏa mãn |z+2w|=4,|z-2w|=2,|3z+w|=3. Tìm giá trị của biểu thức P=$\overline{\mathrm{z} }\mathrm{w}+\mathrm{z}\overline{\mathrm{w}}.$

Cho  hàm số $\mathrm{y}={\mathrm{x}}^3+2(\mathrm{m}+1){\mathrm{x}}^2+3\mathrm{mx}+2$ có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y=-x +2 cắt đồ thị (C ) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2$\sqrt{6}$.

Cho x>0; y>0 thỏa mãn $\ln \left({\mathrm{xy}}^2\right)=8; \ln \frac{\mathrm{x}}{\mathrm{y}}=-1$. Tính P=ln⁡(xy).

Cho hàm số $\mathrm{y}={\mathrm{ax}}^3+{\mathrm{bx}}^2+\mathrm{cx}+\mathrm{d}$ (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:

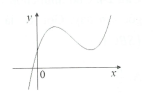
Khẳng định nào sau đây là khẳng định đúng?  

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x–y+z -1= 0 và (Q):2x+y+1= 0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng  (P) và (Q).

Biết $\frac{\mathrm{a}}{\mathrm{b}}$ (trong đó $\frac{\mathrm{a}}{\mathrm{b}}$  là phân số tối giản, a,b∈ ${\mathrm{N}}^{*}$) là giá trị thực của tham số m để hàm số  $\mathrm{y}=2{\mathrm{x}}^3-3{\mathrm{mx}}^2-6(3{\mathrm{m}}^2-1)\mathrm{x}+2018$ có hai điểm cực trị x1;x2 thỏa mãn ${\mathrm{x}}_1{\mathrm{x}}_2+2({\mathrm{x}}_1+{\mathrm{x}}_2)=1$. Tính P= a+2b.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=2a và vuông góc với đáy. Gọi M, N lần lượt là trung điểm của CD và SA. Tính sin góc tạo bởi đường thẳng MN và mặt phẳng (SBD).

Cho các số thực x,y thay đổi thỏa mãn${\log }_2\frac{\mathrm{sinx}+2}{\mathrm{cosx}+2}=2\mathrm{cosx}-\mathrm{sinx}+3$. Gọi -$\frac{\mathrm{a}}{\mathrm{b}} \mathrm{với} \mathrm{a}\in \mathrm{N}*,\mathrm{b}\in \mathrm{N}*,\frac{\mathrm{a}}{\mathrm{b}}$ tối giản là giá trị nhỏ nhất của biểu thức P=$3{\cos }^3\mathrm{x}+\sin 2\mathrm{x}-5\mathrm{cosx}$. Tính T=a+b. 

Biết ${\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=3$ và${\int }_{\mathrm{b}}^{\mathrm{a}}\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}=5$. Tính I=${\int }_{\mathrm{a}}^{\mathrm{b}}\left[3\mathrm{f}\right(\mathrm{x})+2\mathrm{g}(\mathrm{x}\left)\right]\mathrm{dx}$

Biết rằng ${\int }_0^{\frac{\mathrm{\pi }}{4}}(2\mathrm{x}+{\cos }^2\mathrm{x})\mathrm{dx}={\mathrm{a\pi }}^2+\mathrm{b\pi }+\mathrm{c}$, với a,b,c là các số hữu tỉ. Tính P=$\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{1}{\mathrm{c}}$.