Trong tất cả các cặp \(\left( {x;y} \right)\) thỏa mãn \({\log _{{x^2} + {y^2} + 2}}\left( {2x - 4y + 6} \right) \ge 1\). Tìm \(m\) để tồn tại duy nhất một cặp \(\left( {x;y} \right)\) sao cho \({x^2} + {y^2} + 2x - 2y + 2 - m = 0\).
A. \(\sqrt {13} - 3\) và \(\sqrt {13} - 3\).
B. \(\sqrt {13} - 3\).
C. \({\left( {\sqrt {13} - 3} \right)^2}\).
D. \({\left( {\sqrt {13} - 3} \right)^2}\) và \({\left( {\sqrt {13} + 3} \right)^2}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: \({\log _{{x^2} + {y^2} + 2}}\left( {2x - 4y + 6} \right) \ge 1 \Leftrightarrow 2x - 4y + 6 \ge {x^2} + {y^2} + 2 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} \le 9\,\,\,\,\,\left( 1 \right)\)
Giả sử \(M\left( {x;y} \right)\) thỏa mãn \(\left( 1 \right)\), khi đó tập hợp điểm \(M\) là hình tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {1; - 2} \right)\) và bán kính \({R_1} = 3\)
Ta có: \({x^2} + {y^2} + 2x - 2y + 2 - m = 0 \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = m\,\,\,\,\,\left( 2 \right)\)
Nếu \(m < 0\) suy ra \(\left( 2 \right)\) vô nghiệm, do đó \(m < 0\) không thỏa mãn.
Nếu \(m = 0\) suy ra \(\left( 2 \right) \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\), không thỏa mãn \(\left( 1 \right)\).
Nếu \(m >0\) khi đó \(\left( 2 \right)\) là đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( { - 1;1} \right)\) và bán kính \({R_2} = \sqrt m \)
Ta có \({I_1}{I_2} = \sqrt {13} >{R_1} \Rightarrow {I_2}\) nằm ngoài đường tròn \(\left( {{C_1}} \right)\). Vậy để tồn tại duy nhất một cặp \(\left( {x;y} \right)\)thỏa mãn đề bài khi và chỉ khi \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc ngoài hoặc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc trong.
\( \Leftrightarrow \left[ \begin{array}{l}{I_1}{I_2} = {R_1} + {R_2}\\{I_1}{I_2} = {R_2} - {R_1}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt {13} = 3 + \sqrt m \\\sqrt {13} = \sqrt m - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = {\left( {\sqrt {13} - 3} \right)^2}\\m = {\left( {\sqrt {13} + 3} \right)^2}\end{array} \right.\)
Chọn đáp án D
</>
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho\[x\], \[y\], \[z\] là các số thực khác \[0\]thỏa mãn\[{2^x} = {3^y} = {6^{ - z}}\]. Tính giá trị biểu thức \[M = xy + yz + zx\].
Xét \(\int\limits_0^{\frac{\pi }{2}} {\sin x\sqrt {3 + \cos x} } {\rm{d}}x\), nếu đặt \(t = \sqrt {3 + \cos x} \) thì \(\int\limits_0^{\frac{\pi }{2}} {\sin x\sqrt {3 + \cos x} } {\rm{d}}x\) bằng
Có 9 chiếc nghế được xếp thành một hàng ngang. Xếp ngẫu nhiên 9 học sinh gồm 5 học sinh lớp A, 3 học sinh lớp B và 1 học sinh lớp C ngồi vào hàng ghế đó sao cho mỗi ghế có đúng một học sinh. Xác xuất để học sinh lớp C ngồi giữa hai học sinh lớp B là:
Tập nghiệm của bất phương trình \({3.9^x} - {10.3^x} + 3 \le 0\) có dạng\[S = \left[ {a;b} \right]\], trong đó \[a,b\] là các số nguyên. Giá trị của biểu thức \[5b - 2a\] bằng
Trong không gian \[Oxyz\], cho mặt phẳng\((\alpha ):2x + y - z + 1 = 0\). Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng \[(\alpha )\]?
Bất phương trình sau có tất cả bao nhiêu nghiệm nguyên \({4^x} - {33.2^x} + 32 \le 0\).
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Tìm tọa độ điểm biểu diễn số phức \(\frac{{7 - 4i}}{{{z_1}}}\) trên mặt phẳng phức?
Hỏi có bao nhiêu cách xếp bốn bạn An, Bình, Cường, Dũng ngồi vào một bàn học gồm bốn chỗ?
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \({u_5} = 10\). Tính tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\).
Cho tứ diện đều \[ABCD\] có cạnh bằng \[a\]. Gọi \[M,\,\,N\] lần lượt là trung điểm của các cạnh \[AB,\,\,BC\] và \[E\] là điểm đối xứng với \[B\]qua \[D\]. Mặt phẳng \[\left( {MNE} \right)\] chia khối tứ diện \[ABCD\] thành hai khối đa diện. Trong đó, khối tứ diện \[ABCD\]có thể tích là \[V\], khối đa diện chứa đỉnh \[A\] có thể tích \[V'.\] Tính tỉ số \(\frac{{V'}}{V}\).
Có bao nhiêu giá trị nguyên của tham số \(m\) trên \(\left[ { - 2020;{\rm{ }}2020} \right]\) để hàm số \(y = {\log _{2020}}\left( {{x^2} - 2x - m + 1} \right)\) có tập xác định là \(\mathbb{R}\)?
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^2 {f\left( x \right)} \,{\rm{d}}x = 9;\int\limits_2^4 {f\left( x \right)\,} {\rm{d}}x = 4\). Tính \(I = \int\limits_0^4 {f\left( x \right)} \,{\rm{d}}x\)?
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ.
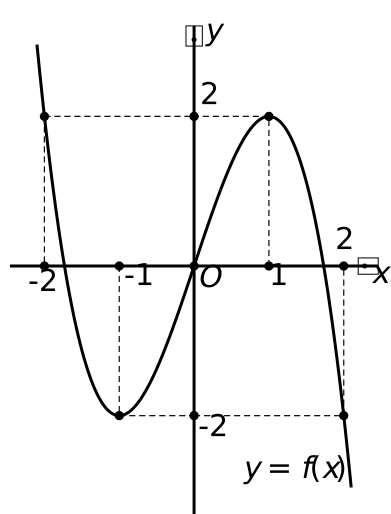
Phương trình \[f\left( {2\cos x} \right) = 2\] có bao nhiêu nghiệm \[x \in \left[ {0;3\pi } \right]\]?