Cho khối chóp S.ABCcó hai điểm \[M,{\rm{ }}N\] lần lượt thuộc hai cạnh \[SA,{\rm{ }}SB\] sao cho \[MA = 2MS,{\rm{ }}NS = 2NB.\] Mặt phẳng \[\left( \alpha \right)\] qua hai điểm M, N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích t của hai khối đa diện đó, biết \[t < 1.\]
A.\[\frac{3}{5}\].
B.\[\frac{4}{9}\].
C.\[\frac{3}{4}\].
D.\[\frac{4}{5}\].
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Chọn đáp án D
Thiết diện là tứ giác MNPQnhư hình vẽ với \(NP{\rm{ // MQ // SC}}\).
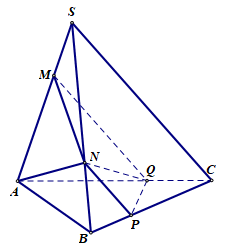
Ta có \({V_{MNABPQ}} = {V_{N.ABPQ}} + {V_{N.AMQ}}\).
+ \({V_{N.ABPQ}} = \frac{1}{3}d\left( {N;\left( {ABC} \right)} \right).{S_{ABPQ}} = \frac{1}{3}.\frac{1}{3}d\left( {S;\left( {ABC} \right)} \right).\left( {{S_{ABC}} - {S_{CPQ}}} \right).\)
+ \(\frac{{{S_{CPQ}}}}{{{S_{CBA}}}} = \frac{{CP}}{{CB}}.\frac{{CQ}}{{CA}} = \frac{2}{3}.\frac{1}{3} \Rightarrow {S_{CPQ}} = \frac{2}{9}{S_{ABC}} \Rightarrow {V_{N.ABPQ}} = \frac{1}{9}d\left( {S;\left( {ABC} \right)} \right).\frac{7}{9}{S_{ABC}} = \frac{7}{{27}}{V_{S.ABC}}.\)
\({V_{N.AMQ}} = \frac{1}{3}d\left( {N;\left( {AMQ} \right)} \right).{S_{AMQ}} = \frac{1}{3}.\frac{2}{3}d\left( {B;\left( {SAC} \right)} \right).\frac{4}{9}{S_{SAC}} = \frac{8}{{27}}{V_{S.ABC}}\)
\( \Rightarrow {V_{MNABPQ}} = {V_{N.ABPQ}} + {V_{N.AMQ}} = \frac{5}{9}{V_{S.ABCD}} \Rightarrow {V_{SMNPCQ}} = \frac{4}{9}{V_{S.ABCD}} \Rightarrow t = \frac{{{V_{SMNPCQ}}}}{{{V_{MNABPQ}}}} = \frac{4}{5}.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho điểm M thuộc mặt cầu (S) có phương trình \[{\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 9\] và ba điểm \[A\left( {1;0;0} \right)\], \[B\left( {2;1;3} \right)\]; \[C\left( {0;2; - 3} \right)\]. Biết rằng quỹ tích các điểm M thỏa mãn \[M{A^2} + 2\overrightarrow {MB} .\overrightarrow {MC} = 8\] là một đường tròn cố định, tính bán kính r đường tròn này.
Cho hàm số \[f\left( x \right) = \frac{{{2^x}}}{{{2^x} + 2}}\]. Tính tổng \[f\left( 0 \right) + f\left( {\frac{1}{{10}}} \right) + ... + f\left( {\frac{{19}}{{10}}} \right)\].
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \left| {{x^4} - 4{x^3} - 8{x^2} - m} \right|\] có đúng 7 điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \frac{{m\sin x - 9}}{{\sin x - m}}\] đồng biến trên khoảng \[\left( {0;\frac{\pi }{2}} \right)\]?
Tính đạo hàm của hàm số \[y = {\log _{\frac{2}{3}}}\sqrt {{x^2} + 1} .\]
Biết rằng \[\int\limits_1^2 {x{{\left( {x - 1} \right)}^n}dx} = \frac{{27}}{{182}},\] với \[n \in {\mathbb{N}^*}.\] Mệnh đề nào dưới đây là đúng?
Trong không gian Oxyz,cho hai vectơ \[\vec u = \left( {1;0;2} \right)\] và \[\vec v = \left( { - 1;2;0} \right).\] Tính \[P = \cos \left( {\vec u;\vec v} \right).\]
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} - {z_2}\] có phần ảo bằng
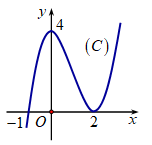
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - y + z - 6 = 0\] và đường thẳng \[d:\frac{{x + 2}}{2} = \frac{{y - 1}}{1} = \frac{{z - 1}}{{ - 1}}.\] Viết phương trình đường thẳng Δ cắt mặt phẳng (P) và đường thẳng d lần lượt tại M và N sao cho \[A\left( {3;5;2} \right)\] là trung điểm của cạnh MN.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SABvuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Côsin của góc giữa mặt phẳng (SCD) và (ABCD) bằng