Cho , tìm số cách chọn một tập con của S gồm 26 phần tử sao cho tổng các phần tử của nó chia hết cho 5
A. 15141523
B. 14121492
C. 1321250
D. 131213
 Giải bởi Vietjack
Giải bởi Vietjack
Cách giải:
Trong tập hợp S ta có:
- Tập hợp các số chia hết cho 5 là 7 phần tử
- Tập hợp các số chia cho 5 dư 1 là 7 phần tử.
- Tập hợp các số chia cho 5 dư 2 là 7 phần tử.
- Tập hợp các số chia cho 5 dư 3 là 7 phần tử.
- Tập hợp các số chia cho 5 dư 4 là 7 phần tử.
Gọi X là tập hợp các tập hợp gồm tất cả các tập con chứa 26 phần tử của S ta có .
Gọi những số chia hết cho 5}, = {những số choc ho 5 dư 1}, {những số chia cho 5 dư 2}, {những số chia cho 5 dư 3}, {những số chia cho 5 dư 4}.
Ta chứng minh được
Vậy số cách chọn một tập con của S gồm 26 phần tử sao cho tổng các phân tử của nó chia hết cho 5 là
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tính thể tích của khối cầu biết chu vi đường tròn lớn của nó bằng
Một sợi dây kim loại dài 120cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành hình vuông, đoạn dây thứ hai được uốn thành vòng tròn (tham khảo hình bên dưới)
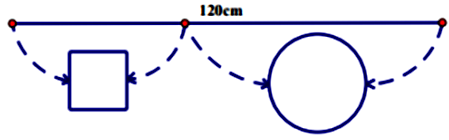
Tổng diện tích của hình vuông và hình tròn đạt giá trị nhỏ nhất là (làm tròn đến hàng đơn vị)
Một đoàn tàu gồm 12 toa chở khách (mỗi toa có thể chứa tối đa 12 khách). Có 7 hành khách chuẩn bị lên tàu. Tính xác suất để đúng 3 toa có người (làm tròn đến chữ số thập phân thứ ba)
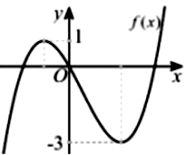
Cho hàm số bậc ba có đồ thị như hình vẽ sau. Có bao nhiêu số dương trong các số a,b,c,d?
Cho khối tứ diện đều ABCD. Gọi M,N lần lượt là trung điểm của AB,CD. Sử dụng mặt phẳng trung trực của AB và mặt phẳng trung trực của CD ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây?
Với mọi hàm số f(x);g(x) liên tục trên cho các khẳng định sau:
(I)
(II)
(III) Nếu thì
(IV) với mọi hằng số
Có bao nhiêu khẳng định sai?