Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và . Gọi H,K,L lần lượt là hình chiếu vuông góc của A lên SB,SC,SD. Xét khối nón (N) có đáy là đường tròn ngoại tiếp tam giác HKL và có đỉnh thuộc mặt phẳng (ABCD). Tính thể tích của khối nón (N).
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
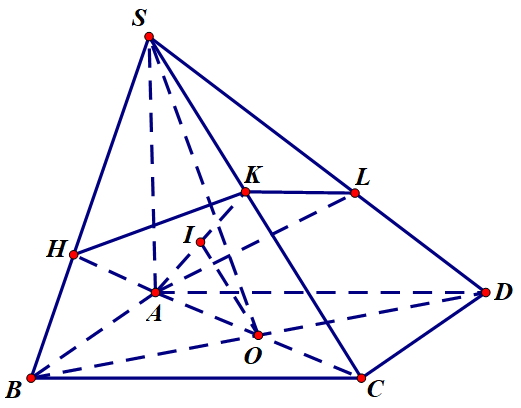
Ta có , mà nên , từ đó suy ra .
Tương tự ta cũng có , từ đó suy ra và tứ giác AHKL nội tiếp đường tròn (C) đường kính AK và nằm trong mặt phẳng (HKL). Do đó (C) chính là đường tròn đáy của khối nón (N).
Gọi , I là trung điểm của AK, suy ra OI là đường trung bình của tam giác AKC nên do đó O là đỉnh của khối nón (N).
Do nên tam giác SAC vuông cân tại A và .
(N) có bán kính đáy , có đường cao .
Thể tích khối nón (N) là .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho a,b,c là các số thực dương khác 1 thỏa mãn , . Khi đó bằng
Biết hàm số đạt giá trị lớn nhất là M, giá trị nhỏ nhất là m. Tổng M+m là
Một lớp có 25 học sinh nam và 10 học sinh nữ. Số cách chọn 3 em học sinh trong đó có nhiều nhất 1 em nữ là:
Cho hình chóp tứ giác đều S.ABCD có cạnh AB=a và SA=2a. Tính tan của góc giữa đường thẳng SA và mặt phẳng (ABCD).
Cho là góc giữa hai vectơ và trong không gian. Khẳng định nào đúng?
Cho f(x) là hàm bậc 4 và có bảng biến thiên như hình vẽ sau:
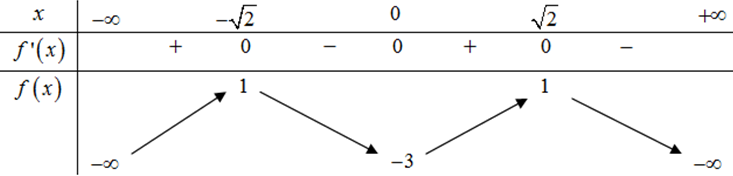
Đồ thị hàm số có mấy đường tiệm cận đứng?