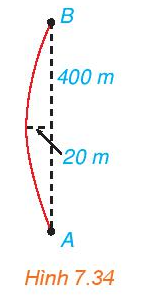
Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B (H.7.34).
a) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế.
b) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Chọn hệ trục tọa độ Oxy sao cho đỉnh của parabol trùng với gốc tọa độ O(0; 0) (như hình vẽ).
Gọi H là hình chiếu của O lên AB, khi đó ta chứng minh được H là trung điểm của AB nên HA = HB = 1/2AB.
Khoảng cách từ khúc cua đến đường thẳng AB là OH.
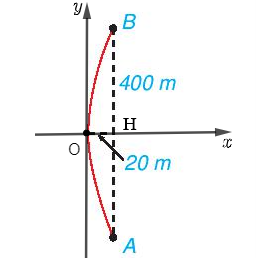
a) Khoảng cách AB = 400 m.
Ta có: HA = HB = 400 : 2 = 200 (m).
OH = 20 m.
Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế thì tọa độ các điểm là: A(20; – 200) và B(20; 200).
Gọi phương trình parabol (P) có dạng y2 = 2px (với p > 0).
Khi đó A, B đều thuộc (P).
Thay tọa độ điểm B vào phương trình parabol (P) ta có: 2002 = 2p . 20 ⇔ 2p = 2000.
Vậy parabol (P) có phương trình là: y2 = 2000x.
b) Đổi: 400 m = 0,4 km; 20 m = 0,02 km.
Khi đó HA = HB = 0,4 : 2 = 0,2 (km).
OH = 0,02 km.
Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế thì tọa độ các điểm là: A(0,02; – 0,2) và B(0,02; 0,2)
Gọi phương trình parabol (P) có dạng y2 = 2p'x (với p' > 0).
Khi đó A, B đều thuộc (P).
Thay tọa độ điểm B vào phương trình parabol (P) ta có: 0,22 = 2p' . 0,02 ⇔ 2p' = 2.
Vậy parabol (P) có phương trình là: y2 = 2x.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thủy thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thủy thuộc đường hybebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.
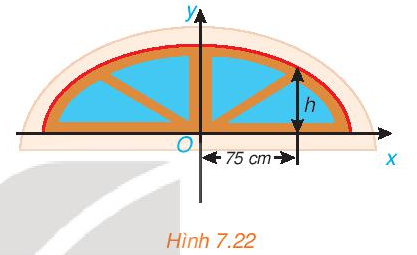
Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình
.
Biết rằng 1 đơn vị trên mặt phẳng tọa độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tính chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.
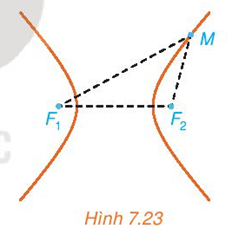
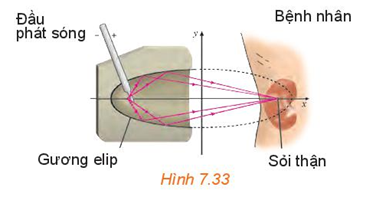
Giả sử thiết bị tại F2 nhận được tín hiệu âm thanh sớm hơn thiết bị tại F1 là 2 giây và vận tốc âm thanh là 343 m/s.
a) Tìm mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F1, F2.
b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh có liên quan đến bài toán tìm tập hợp những điểm M thỏa mãn MF1 – MF2 = 686 (m) hay không?
Gương elip trong một máy tán sỏi thận (H.7.33) ứng với elip có phương trình chính tắc (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.
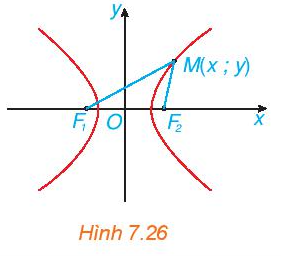
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu tọa độ của các tiêu điểm F1, F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi
. (3)
Cho parabol (P): y = 1/4x2. Xét F(0; 1) và đường thẳng Δ: y + 1 = 0. Với điểm M(x; y) bất kì, chứng minh rằng MF = d(M, Δ) ⇔ M(x; y) thuộc (P).
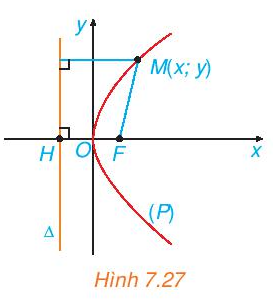
Xét (P) là một parabol với tiêu điểm F và đường chuẩn Δ. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên Δ. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF (H.7.27).
a) Nêu tọa độ của F và phương trình của ∆.
b) Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi
Bài 22: Ba đường conic