Cho tam giác ABC có diện tích bằng S = , hai đỉnh A (2; −3) và
B (3; −2). Trọng tâm G nằm trên đường thẳng 3x – y – 8 = 0. Tìm tọa độ đỉnh C?
A. C (−10; −2) hoặc C (1; −1).
B. C (−2; −10) hoặc C (1; −1).
C. C (−2; 10) hoặc C (1; −1).
D. C (2; −10) hoặc C (1; −1).
 Giải bởi Vietjack
Giải bởi Vietjack
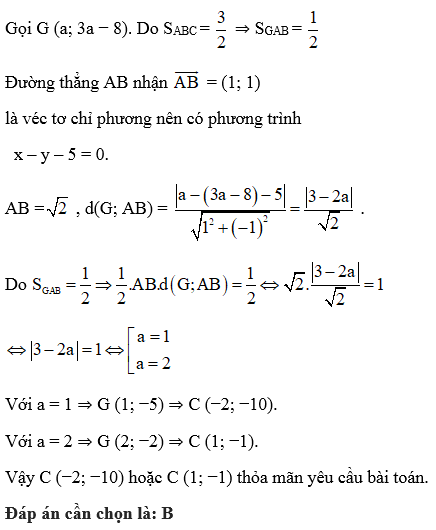
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Viết phương trình đường thẳng đi qua điểm M (2; -3) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân
Xác định m để 2 đường thẳng d: 2x – 3y + 4 = 0 và d’: vuông góc
Lập phương trình đường phân giác trong của góc A của ΔABC biết
A (2; 0); B (4; 1); C (1; 2).
Cho tam giác ABC biết trực tâm H (1; 1) và phương trình cạnh AB:
5x − 2y + 6 = 0, phương trình cạnh AC: 4x + 7y – 21 = 0. Phương trình cạnh BC là
Câu 4. Cho 3 đường thẳng (d1): 3x − 2y + 5 = 0, (d2): 2x + 4y – 7 = 0,
(d3): 3x + 4y – 1 = 0. Viết phương trình đường thẳng (d) đi qua giao điểm của (d1), (d2) và song song với (d3).
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP vuông tại M. Biết điểm M (2; 1), N (3; −2) và P là điểm nằm trên trục Oy. Tính diện tích tam giác MNP.
Trong mặt phẳng với hệ tọa độ Oxy cho ΔABC có A (1; 2), B (4; −2),
C (−3; 5). Một véctơ chỉ phương của đường phân giác trong của góc A là
Với giá trị nào của m thì hai đường thẳng (Δ1): 3x + 4y – 1 = 0 và
(Δ2): (2m − 1)x + m2y + 1 = 0 trùng nhau.
Gọi Δ là đường thẳng song song với đường thẳng d: 3x − 2y + 12 = 0 và cắt Ox, Oy lần lượt tại A, B sao cho . Phương trình nào dưới đây có thể là phương trình của Δ?
Điểm A (a; b) thuộc đường thẳng và cách đường thẳng
Δ: 2x – y – 3 = 0 một khoảng bằng và a > 0. Tính P = a.b
Đường thẳng d: , với đi qua điểm và tạo với các tia Ox, Oy một tam giác có diện tích bằng 4. Tính S = a + 2b
Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng