Cho các số phức z1=1+3i,z2=−5−3i. Tìm điểm M(x;y) biểu diễn số phức z3, biết rằng trong mặt phẳng phức điểm M nằm trên đường thẳng x−2y+1=0 và mô đun số phức w=3z3−z2−2z1 đạt giá trị nhỏ nhất.
A. M(35;15)
B. M(-35;-15)
C. M(35;−15)
D. M(-35;15)
Giải bởi Vietjack
Chọn D.
Trắc nghiệm: Thay tọa độ điểm M vào vế trái phương trình đường thẳng kết quả bằng 0 thỏa ta được đáp án A.
Tự luận:
Ta có w=3z3−z2−2z1=3z3+3−3i=3(z3+1−i)→|w|=3|z3+1−i|=3AM với A(-1;3)
M(x;y) biểu diễn số phức z3 nằm trên đường thẳng d:x−2y+1=0 và A(−1;3)∉d.
Khi đó |w|=3|z3+1−i|=3AM đạt giá trị nhỏ nhất khi AM ngắn nhất ⇔AM⊥d
AM⊥d nên AM có phương trình: 2x+y+1=0.
Khi đó M=AM∩d nên M(−35;15).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y=f(x) có bảng biến thiên như sau:
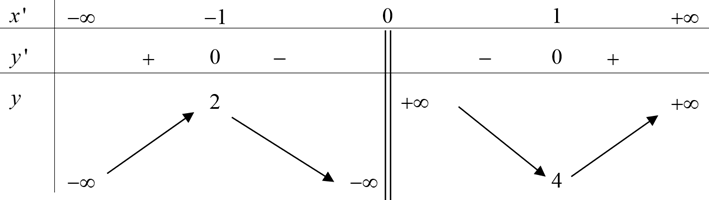
Hàm số nghịch biến trong khoảng nào?
Cho hàm số f(x) liên tục trên ℝ có đồ thị như hình vẽ.
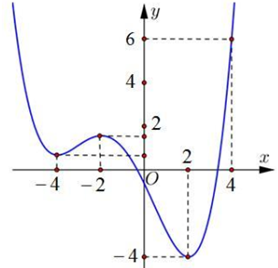
Có tất cả bao nhiêu giá trị nguyên của tham số a để hàm số y=|f(8xx2+1)+a−1| có giá trị lớn nhất không vượt quá 20?
Cho hàm số f(x) có bảng biến thiên như hình vẽ.
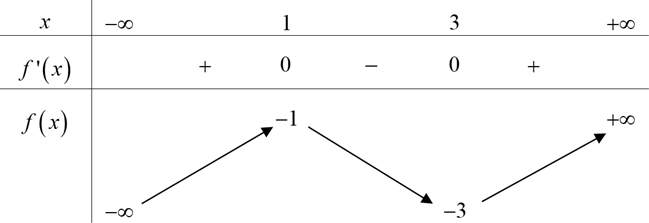
Điểm cực đại của hàm số đã cho là:
Cho hàm số bậc bốn y=f(x) có đồ thị là đường cong trong hình bên.
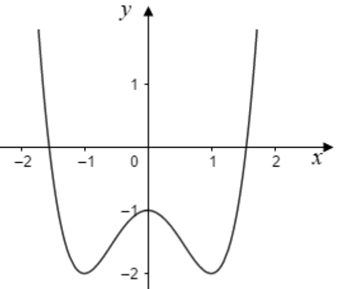
Số nghiệm của phương trình f(x)=−12 là
Một em bé có bộ 6 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 3 thẻ chữ T, một thẻ chữ N, một thẻ chữ H và một thẻ chữ P. Em bé đó xếp ngẫu nhiên 6 thẻ đó thành một hàng ngang. Tính xác suất em bé xếp được thành dãy TNTHPT
Trong không gian Oxyz cho mặt cầu (S):x2+y2+z2−4x+2y−6z+1=0. Tọa độ tâm I của mặt cầu là
Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA⊥(ABC). Mặt phẳng (SBC) cách A một khoảng bằng a và hợp với mặt phẳng (ABC) góc 300. Thể tích của khối chóp S.ABC bằng
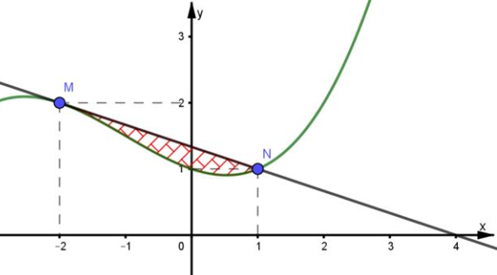
Cho f(x) là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm M có hoành độ bằng -2 cắt đồ thị tại điểm thứ hai N(1;1) cắt Ox tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là 916. Tích phân 1∫−1f(x)dx bằng
Có bao nhiêu bộ (x;y) với x,y nguyên và 1≤x,y≤2020 thỏa mãn (xy+2x+4y+8)log3(2yy+2)≤(2x+3y−xy−6)log2(2x+1x−3)?
