Cho hàm số . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là: y = f'(x0).(x - x0) + y0
Cách giải:
![]()
Tiếp tuyến của (C) vuông góc với đường thẳng d: y = x nên tiếp tuyến có hệ số góc k = -1
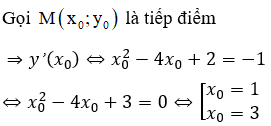
![]()
=> Phương trình tiếp tuyến
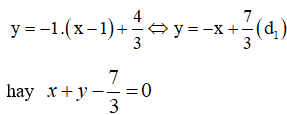
![]()
=> Phương trình tiếp tuyến
![]()
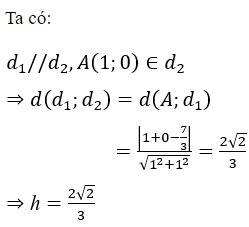
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.
Cho khối tứ diện ABCD, M là trung điểm của AB. Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện nào?
Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?
Ông A gửi vào ngân hàng 100 triệu đồng theo hình thức lãi suất kép. Lãi suất ngân hàng là 8% trên năm và không thay đổi qua các năm ông gửi tiền. Sau 5 năm ông cần tiền sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông tiếp tục gửi ngân hàng và với hình thức như trên. Hỏi sau 10 năm ông A đã thu được số tiền lãi là bao nhiêu? (đơn vị tính là triệu đồng).
Cho hàm số có đồ thị (C). Đồ thị (C) có bao nhiêu đường tiệm cận?
Cho lăng trụ đứng có đáy ABC là tam giác vuông cân tại C, Biết tam giác ABC1 có chu vi bằng 5a . Tính thể tích V của khối lăng trụ
Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của đỉnh S lên đáy là trung điểm của AB, cạnh bên SC tạo với đáy một góc 450. Tính thể tích V của khối chóp đã cho.
Cho hàm số (với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
Đồ thị hàm số có tiệm cận đứng x = a và tiệm cận ngang y = b. Tính giá trị
Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.