Số phức z thỏa mãn: là
A. 2 + i.
B. -2 - i.
C. -3 - i.
D. 2 - i
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D.
![]()
![]()
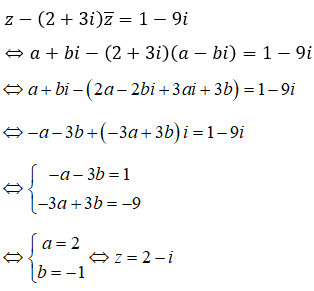
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết