Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Cách 1:
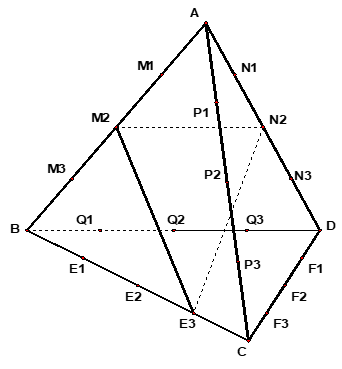
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. = 6 cách.
Suy ra số tam giác thỏa mãn là - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
Cách 2: Lưu Thêm
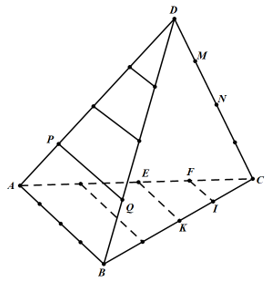
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có cách.
Trong số đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 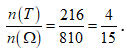
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tổ có 5 học sinh nữ và 6 học sinh nam. Xếp ngẫu nhiên các học sinh trên thành hàng ngang để chụp ảnh. Tính xác suất để không có hai học sinh nữ nào đứng cạnh nhau.
Trên kệ sách có 10 cuốn sách Toán và 5 cuốn sách Văn. Người ta lấy ngẫu nhiên lần lượt 3 cuốn sách mà không để lại. Tính xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn.
Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Tính xác suất chọn được một học sinh nữ.
Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cần chọn ra 2 bạn trong tổ 1 để phân công trực nhật. Xác suất để chọn được 1 bạn nam và 1 bạn nữ là
Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là
Cho n và k là hai số nguyên dương tùy ý thỏa mãn k n mệnh đề nào dưới đây đúng?
Xét một phép thử có không gian mẫu và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ?
Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong ![]() quả cầu lấy được có đúng 4 quả cầu vàng.
quả cầu lấy được có đúng 4 quả cầu vàng.
Một hộp đựng 7 viên bi đỏ đánh số từ 1 đến 7 và 6 viên bi xanh đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
Cho tập hợp A có 20 phần tử. Có bao nhiêu tập con của A khác rỗng và số phần tử là số chẵn?
Cho tập hợp S = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên ba số từ tập S. Tính xác suất của biến cố trong ba số được chọn ra không chứa hai số nguyên liên tiếp nào.
Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh khối 10, 5 học sinh khối 11 và 3 học sinh khối 12 thành một hàng ngang. Xác suất để không có học sinh khối 11 nào xếp giữa hai học sinh khối 10 bằng
Xếp ngẫu nhiên 4 quyển sách Toán khác nhau và 4 quyển sách Hóa giống nhau vào một giá sách nằm ngang có 10 ô trống, mỗi quyển sách được xếp vào một ô. Xác suất để 4 quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau bằng
Lấy ngẫu nhiên một số nguyên dương không vượt quá 10000. Xác suất để số lấy được là bình phương của một số tự nhiên bằng? (tính dưới dạng %)
Tại SEA Games 2019, môn bóng chuyền nam có 8 đội bóng tham dự, trong đó có hai đội Việt Nam và Thái Lan. Các đội bóng được chia ngẫu nhiên thành hai bảng có số đội bóng bằng nhau. Xác suất để hai đội Việt Nam và Thái Lan nằm ở hai bảng khác nhau bằng: