299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P6)
-
2778 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho n và k là hai số nguyên dương tùy ý thỏa mãn k n mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn B
Theo công thức tính của ![]() ta có:
ta có:
![]()
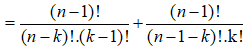
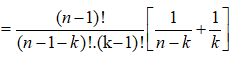
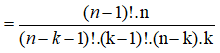
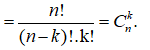
Vậy
Câu 2:
Có bao nhiêu số nguyên dương n nghiệm đúng bất phương trình
 Xem đáp án
Xem đáp án
Chọn B
Ta có: 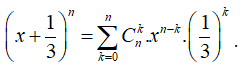
Cho x = 1, ta có:
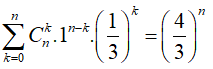
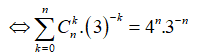
![]()
![]()
Mà ![]()
![]()
Suy ra: ![]()
![]()
![]()
Mà ![]()
Vậy có 1002 số nguyên dương n nghiệm đúng bất phương trình.
Câu 3:
Cho khai triển thỏa mãn . Giá trị của số nguyên dương n bằng:
 Xem đáp án
Xem đáp án
Chọn A
Ta có: 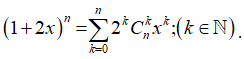
Suy ra: ![]()
Thay ![]()
![]()
vào giả thiết ta có: ![]()
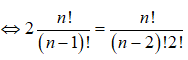
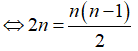
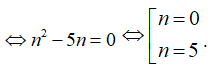
Câu 5:
Cho . Tính T = ?
 Xem đáp án
Xem đáp án
Chọn A
Ta có ![]()
![]()
![]()
![]()
![]()
![]()
Ta có ![]()
![]()
Đạo hàm hai vế ta được: ![]()
![]()
![]()
![]()
Đạo hàm 2 vế ta được: 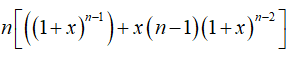
![]()
Thay x = 1 vào 2 vế : ![]()
![]()
Với n = 10, T = ![]()
![]()
![]()
Câu 6:
Cho tập hợp A có 20 phần tử. Có bao nhiêu tập con của A khác rỗng và số phần tử là số chẵn?
 Xem đáp án
Xem đáp án
Chọn B
Số tập hợp con của A khác rỗng có số phần tử là số chẵn là:
![]()
Để tính M ta xét: ![]()
![]()
Thay x = 1 ta có: ![]()
![]()
Thay x = -1 ta có: ![]()
![]()
Từ (1) và (2) ta có:
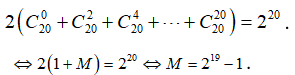
Câu 8:
Xét một phép thử có không gian mẫu và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ?
 Xem đáp án
Xem đáp án
Chọn D
Theo định nghĩa biến cố chắc chắn ta có: Với A là biến cố chắc chắn thì n(A) = n()
Suy ra: 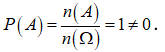 .
.
Câu 9:
Cho phép thử là “gieo 2019 đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa của các đồng xu. Khi đó số phần tử của không gian mẫu bằng
 Xem đáp án
Xem đáp án
Chọn C
Ta có: ![]()
![]()
Vì một đồng xu có hai mặt nên khi gieo 2019 đồng xu phân biệt ta có kết quả có thể xảy ra của phép thử. Vậy số
phần tử của không gian mẫu là n() = .
Câu 10:
Cho phép thử là “gieo 10 con súc sắc cân đối, đồng chất phân biệt”. Khi đó số phần tử của không gian mẫu bằng
 Xem đáp án
Xem đáp án
Chọn D
Câu 11:
Cho phép thử là “gieo 10 đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa của các đồng xu. Xác suất để có đúng một lần suất hiện mặt ngửa là
 Xem đáp án
Xem đáp án
Chọn A
Ghi nhớ:
-Phép thử “gieo hai đồng tiền phân biệt” thì hai kết quả SN, NS của phép thử là khác nhau.
-Phép thử “gieo n đồng xu phân biệt” thì không gian mẫu có phần tử, với n .
Câu 12:
Gieo một con súc sắc cân đối và đồng chất. Giả sử súc sắc xuất hiện mặt b chấm. Xác suất để phương trình + 2bx + 4 = 0 có nghiệm là
 Xem đáp án
Xem đáp án
Chọn D
Theo đề bài b là số chấm của con súc sắc nên b{1;2;3;4;5;6}
Để phương trình + 2bx + 4 = 0 có nghiệm thì ![]()
Kết hợp b[1;6] suy ra b{2;3;4;5;6} Suy ra xác suất để phương trình
+ 2bx + 4 = 0 có nghiệm là
Câu 13:
Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cần chọn ra 2 bạn trong tổ 1 để phân công trực nhật. Xác suất để chọn được 1 bạn nam và 1 bạn nữ là
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu ![]()
Gọi biến cố A: “Chọn được 1 bạn nam và 1 bạn nữ để phân công trực nhật.”
Ta có ![]()
Vậy ![]()
Câu 14:
Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong ![]() quả cầu lấy được có đúng 4 quả cầu vàng.
quả cầu lấy được có đúng 4 quả cầu vàng.
 Xem đáp án
Xem đáp án
Chọn C
Chọn 4 quả cầu từ 10 quả cầu có (cách ) ![]() .
.
Gọi A là biến cố “4 quả cầu lấy được có đúng 2 quả màu vàng”.
Chọn 4 quả cầu trong đó có đúng 2 quả màu vàng có => n(A) =
Xác suất của biến cố A là: 
Câu 15:
Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số. Tính xác suất để số được chọn có ít nhất hai chữ số 8 đứng liền nhau.
 Xem đáp án
Xem đáp án
Chọn A
Xét phép thử: “Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số”
Ta có ![]()
Biến cố A: “Số được chọn có ít nhất hai chữ số 8 đứng liền nhau”.
Gọi số có 4 chữ số là trong đó có ít nhất hai chữ số 8 đứng liền nhau, a0
TH1: Có đúng hai chữ số 8 đứng liền nhau.
+) Số có dạng : có 9.9 = 81 số.
+) Số có dạng hoặc : mỗi dạng có 8.9 = 72 số.
TH2: Có đúng ba chữ số 8 trong đó có ít nhất hai chữ số 8 đứng liền nhau.
+) Số có dạng : có 8 số.
+) Số có dạng hoặc hoặc : Mỗi dạng có 9 số.
TH3: Cả 4 chữ số đều là chữ số 8: Có 1 số là số 8888
Do đó n(A) = 81 + 2.72 + 8 + 3.9 + 1 = 261
Xác suất cần tìm 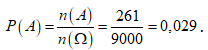
Câu 16:
Tại SEA Games 2019, môn bóng chuyền nam có 8 đội bóng tham dự, trong đó có hai đội Việt Nam và Thái Lan. Các đội bóng được chia ngẫu nhiên thành hai bảng có số đội bóng bằng nhau. Xác suất để hai đội Việt Nam và Thái Lan nằm ở hai bảng khác nhau bằng:
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử không gian mẫu là số cách chia 8 đội bóng vào hai bảng sao cho mỗi bảng có 4 đội
![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Ta có: ![]()
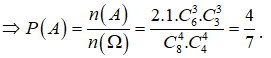
Câu 17:
Trên kệ sách có 10 cuốn sách Toán và 5 cuốn sách Văn. Người ta lấy ngẫu nhiên lần lượt 3 cuốn sách mà không để lại. Tính xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn.
 Xem đáp án
Xem đáp án
Chọn D
Lấy lần lượt 3 cuốn sách có 15.14.13 = 2730 cách
Lấy 2 cuốn sách đầu là Toán và cuốn còn lại là Văn có 10.9.5 = 450 cách
Xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn: ![]()
Câu 18:
Cho tập hợp S = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên ba số từ tập S. Tính xác suất của biến cố trong ba số được chọn ra không chứa hai số nguyên liên tiếp nào.
 Xem đáp án
Xem đáp án
Chọn D
Xét phép thử: “Chọn ngẫu nhiên ba số từ tập S = {1;2;3;4;5;6;7;8;9}. Ta có ![]() .
.
Gọi A là biến cố: “trong ba số được chọn ra không chứa hai số nguyên liên tiếp”.
Gọi là ba số thỏa mãn ![]() .
.
Không có hai số nguyên liên tiếp nào ![]() .
.
Đặt ![]() . Khi đó:
. Khi đó: ![]() .
.
Số cách chọn bộ ba số ![]() => có cách chọn
=> có cách chọn
Suy ra ![]()
Do đó 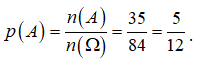
Câu 19:
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
 Xem đáp án
Xem đáp án
Chọn D
Cách 1:
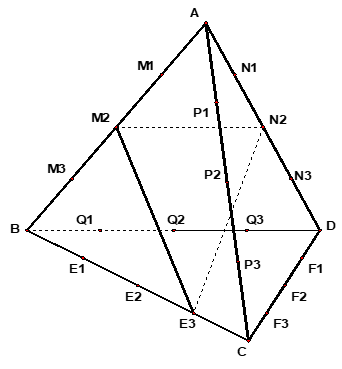
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. = 6 cách.
Suy ra số tam giác thỏa mãn là - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
Cách 2: Lưu Thêm
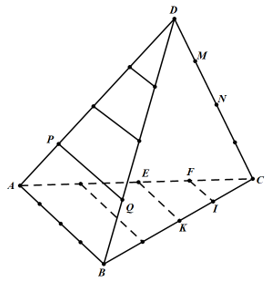
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có cách.
Trong số đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 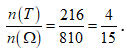
Câu 20:
Xếp ngẫu nhiên 21 học sinh, trong đó có đúng một bạn tên Thêm và đúng một bạn tên Quý vào ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8. Xác suất để hai bạn Thêm và Quý ngồi cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn A
Đánh số ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8 là bàn 1, bàn 2, bàn 3.
+) Xét phép thử: “Xếp ngẫu nhiên 21 học sinh vào ba bàn tròn 1, 2, 3 nói trên”.
Chọn 6 học sinh trong số 21 học sinh và xếp vào bàn 1 có ![]() cách.
cách.
Chọn 7 học sinh trong số 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Suy ra số phần tử của không gian mẫu là ![]()
+) Gọi A là biến cố: “ Hai bạn Thêm và Quý luôn ngồi cạnh nhau ”.
Trường hợp 1: Hai bạn Thêm và Quý ngồi bàn 1.
Chọn 4 học sinh từ 19 học sinh còn lại có cách.
Xếp 4 học sinh vừa chọn và hai bạn Thêm, Quý vào bàn 1 có 4!.2! cách.
Chọn 7 học sinh từ 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Số cách xếp thỏa mãn trường hợp 1 là: ![]()
Trường hợp 2: Hai bạn Thêm và Quý ngồi bàn 2.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 2 là ![]()
Trường hợp 3: Hai bạn Thêm và Quý ngồi bàn 3.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 3 là: ![]()
![]()
![]()
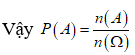
= =
Câu 21:
Xếp ngẫu nhiên 4 quyển sách Toán khác nhau và 4 quyển sách Hóa giống nhau vào một giá sách nằm ngang có 10 ô trống, mỗi quyển sách được xếp vào một ô. Xác suất để 4 quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu là tập hợp tất cả các cách xếp 4 quyển Toán khác nhau và 4 quyển Hóa giống nhau vào 8 trong 10 ô trống.
Khi đó, ![]()
Gọi A là biến cố: “ Bốn quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau ”.
Để xếp 4 quyển sách Toán cạnh nhau và 4 quyển sách Hóa gần nhau trên giá sách 10 ô trống ta xem như có 4 vị trí để xếp
Xếp 4 quyển toán cạnh nhau có 4! cách, xếp 4 quyển Hóa có 1 cách, sau đó xếp 2 bộ đó vào 2 trong 4 vị trí.
Do đó: ![]()
Xác suất để 4 quyển sách Toán cạnh nhau và 4 quyển Hóa cạnh nhau là:

Câu 22:
Gọi S là tập hợp tất cả các số tự nhiên gồm 3 chữ số. Chọn ngẫu nhiên một số thuộc S. Xác suất để số chọn được là một số tự nhiên chia hết cho 9 và có các chữ số đôi một khác nhau bằng
 Xem đáp án
Xem đáp án
Chọn A
+) Không gian mẫu = “Chọn ngẫu nhiên một số trong các số tự nhiên có 3 chữ số”.=> || = 9.
+) Biến cố A = “Số tự nhiên được chọn chia hết cho 9 và các chữ số đôi một khác nhau”.
Ta tìm số các số tự nhiên gồm 3 chữ số khác nhau và chia hết cho 9 (tổng các chữ số là một số chia hết cho 9).
Bộ ba số (a;b;c) với a,b,c [0;9](a,b,c đôi một khác nhau ) và a + b + c = 9m, m được liệt kê dưới đây:

Vậy có tất cả 10.3! + 4.2.2! = 76 => = 76
Xác suất cần tính bằng 
Câu 23:
Có một dãy ghế gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh gồm 2 học sinh lớp A, 2 học sinh lớp B, 2 học sinh lớp C ngồi vào dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để không có học sinh lớp C nào ngồi cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn A
Số cách xếp ngẫu nhiên 6 học sinh vào dãy ghế: = 6!.
Gọi M là biến cố “xếp 6 học sinh vào dãy ghế mà không có học sinh lớp C nào ngồi cạnh nhau”.
Gọi là biến cố “xếp 6 học sinh vào dãy ghế mà hai học sinh lớp C ngồi cạnh nhau”.
Ghép 2 học sinh lớp C thành nhóm X.
Xếp nhómX, 2 học sinh lớp A, 2 học sinh lớp B vào dãy ghế: 5!.
Hoán đổi vị trí 2 học sinh lớp C: 2!.
![]()
Vậy ![]()
Câu 24:
Một tổ có 5 học sinh nữ và 6 học sinh nam. Xếp ngẫu nhiên các học sinh trên thành hàng ngang để chụp ảnh. Tính xác suất để không có hai học sinh nữ nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn C
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 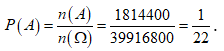
Câu 25:
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng?
 Xem đáp án
Xem đáp án
Chọn A
Cách 1:
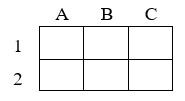
Số phần tử không gian mẫu là 6! = 720.
Xếp bạn nam thứ nhất có 6 cách, bạn nam thứ 2 có 4 cách, bạn nam thứ 3 có 2 cách.
Xếp 3 bạn nữ vào ba ghế còn lại có ![]() cách.
cách.
Vậy xác suất cần tìm là ![]() . Đáp án A.
. Đáp án A.
Câu 26:
Gọi S là tập hợp tất cả các số tự nhiên gồm 9 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ số lẻ (các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ).
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu là ![]()
Gọi số cần tìm là ![]()
* Trường hợp = 0: Khi đó lẻ nên có cách xếp, hai chữ số lẻ còn lại có cách xếp, 4 chữ số chẵn còn lại có 4! cách xếp. Vậy theo quy tắc nhân có
.4! = 43200 (số)
Vậy xác suất cần tính là: ![]()
Câu 27:
Giải bóng chuyền VTV Cup có 12 đội tham dự trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng đấu A, B, C, mỗi bảng đấu có 4 đội. Xác suất để 3 đội Việt Nam ở 3 bảng đấu khác nhau là
 Xem đáp án
Xem đáp án
Chọn C
Không gian mẫu :” Chia 12 đội thành 3 bảng mỗi bảng 4 đội”
![]() .
.
Gọi biến cố A:” 3 đội Việt Nam ở 3 bảng đấu khác nhau”.
+ Có 3! cách xếp 3 đội Việt Nam vào 3 bảng đấu.
+ Có cách xếp 9 đội nước ngoài vào 3 bảng đấu.
![]() . Vậy xác suất cần tìm là
. Vậy xác suất cần tìm là ![]() .
.
Câu 28:
Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh khối 10, 5 học sinh khối 11 và 3 học sinh khối 12 thành một hàng ngang. Xác suất để không có học sinh khối 11 nào xếp giữa hai học sinh khối 10 bằng
 Xem đáp án
Xem đáp án
Chọn D
“Xếp 10 học sinh thành một hàng ngang” => n() = 10!
A “Không có học sinh khối 11 nào xếp giữa hai học sinh khối 10”.
Trường hợp I (2 học sinh khối 10 đứng cạnh nhau):
Bước 1: Buộc 2 học sinh khối 10 thành một phần tử X và đổi chỗ 2 học sinh đó có 2! cách.
Bước 2: Xếp phần tử X và 8 học sinh còn lại thành một hàng ngang có 9! cách.
Vậy, có 9!.2! cách.
Trường hợp II (giữa 2 học sinh khối 10 có 1 học sinh khối 12):
Bước 1: Chọn 1 học sinh khối 12 trong 3 học sinh có cách.
Bước 2: Buộc 2 học sinh khối 10 và học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10 có 2! cách.
Bước 3: Xếp phần tử X và 7 học sinh còn lại thành một hàng ngang có 8! cách.
Vậy, có .2!.8! cách.
Trường hợp III (giữa 2 học sinh khối 10 có 2 học sinh khối 12):
Bước 1: Chọn 2 học sinh khối 12 trong 3 học sinh có cách.
Bước 2: Buộc 2 học sinh khối 10 và 2 học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10, đổi chỗ 2 học sinh khối 12 có 2!.2! cách.
Bước 3: Xếp phần tử X và 6 học sinh còn lại thành một hàng ngang có 7! cách.
Vậy, có .2!.2!.7!cách.
Trường hợp IV (giữa 2 học sinh khối 10 có 3 học sinh khối 12):
Bước 1: Buộc 2 học sinh khối 10 và 3 học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10, đổi chỗ 3 học sinh khối 12 có 2!.3! cách.
Bước 2: Xếp phần tử X và 5 học sinh còn lại thành một hàng ngang có 6! cách.
Vậy, có 2!.3!.6! cách.
Theo quy tắc cộng, ta được ![]()
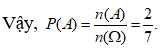
Câu 29:
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 4”. Tính xác suất P(A) của biến cố A
 Xem đáp án
Xem đáp án
Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n() = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n )
* Ta có ![]() suy ra
suy ra ![]() Do đó
Do đó 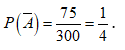
![]()
Câu 30:
Gọi S là tập hợp các số tự nhiên, mỗi số không có quá 3 chữ số và tổng các chữ số bằng 9. Lấy ngẫu nhiên một số từ ![]() . Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
. Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
 Xem đáp án
Xem đáp án
Chọn A
- Bổ đề: Cho ![]() , ta có:
, ta có:
“Số nghiệm nguyên không âm của phương trình ![]()
Thật vậy: Đặt ![]()
Khi đó ![]() và
và ![]()
Hiển nhiên số nghiệm nguyên không âm của (1) bằng số nghiệm nguyên dương của (2)
- Xếp m + n chữ số 1 thành một hàng: có 1 cách.
- Xếp n - 1 dấu gạch ngang "-" vào trong m + n -1 khoảng trống giữa các chữ số 1 (mỗi khoảng trống nhiều nhất một dấu gạch ngang) để chia dãy m + n chữ số 1 thành n phần (mỗi phần có ít nhất một chữ số 1): có cách.
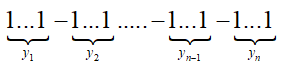
Mỗi phần được chia ra có tổng các chữ số 1 lần lượt là ![]()
và cho ta một nghiệm nguyên dương của phương trình (2).
Do đó số nghiệm nguyên dương của phương trình (2) là ![]()
Suy ra số nghiệm nguyên không âm của phương trình (1) là (đpcm)
Bây giờ ta sẽ áp dụng kết quả của bổ đề để giải bài toán đã cho:
- Tính số phần tử của tập S:
Gọi phần tử của S là vơí ![]() và a + b + c = 9 (*)
và a + b + c = 9 (*)
Theo bổ đề thì số nghiệm nguyên không âm của (*) là ![]()
Vậy n(S) = 55
- Tính số các phần tử của S có chữ số hàng trăm bằng 4.
Khi đó a= 4 và b + c = 5 (**).
Theo bổ đề thì số nghiệm nguyên không âm của (**) là ![]()
Vậy có tất cả 6phần tử của S có chữ số hàng trăm bằng 4.
- Xét phép thử: “Lấy ngẫu nhiên một số từ tập S” và biến cố A: “Số lấy ra có chữ số hàng trăm bằng 4”
Ta có ![]()
Vậy xác suất của biến cố A là 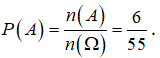
Câu 31:
Gọi n(A) là số các kết quả thuận lợi cho biến cố liên quan đến một phép thử T và là số các kết quả có thể xảy ra của phép thử T đó. Xác suất P() của biến cố đối của biến cố A không là đẳng thức nào trong các đẳng thức sau?
 Xem đáp án
Xem đáp án
Chọn A
Ta có 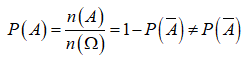
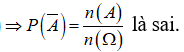
Câu 32:
Với các chữ “LẬP”, “HỌC”, “MAI”, “NGÀY”, “NGHIỆP”, “TẬP”, “VÌ”, mỗi chữ được viết lên một tấm bìa, sau đó người ta trải ra ngẫu nhiên. Xác suất để được dòng chữ “HỌC TẬP VÌ NGÀY MAI LẬP NGHIỆP” bằng:
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử không gian mẫu khi xếp ngẫu nhiên 7 miếng bìa là: = 7!
Số cách xếp để được dòng chữ “HỌC TẬP VÌ NGÀY MAI LẬP NGHIỆP” là n(A) = 1

Câu 33:
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn chấm?
 Xem đáp án
Xem đáp án
Chọn C
Gọi A là biến cố “ Súc sắc xuất hiện mặt chẵn chấm”
![]()
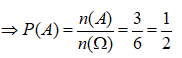
Câu 34:
Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là:
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu là: ![]()
Gọi A là biến cố: “Mặt có số chấm chẵn xuất hiện”.
![]()
Xác suất để mặt có số chấm chẵn xuất hiện là:
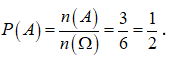
Câu 35:
Trong một lớp học gồm 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học sinh lên giải bài tập. Tính xác suất để 4 học sinh được gọi đó có cả nam và nữ?
 Xem đáp án
Xem đáp án
Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
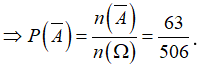
Vậy xác suất của biến cố A là
![]()
Câu 36:
Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Tính xác suất chọn được một học sinh nữ.
 Xem đáp án
Xem đáp án
Chọn B
Ta có: ![]()
Gọi A là biến cố: “Chọn được một học sinh nữ”.
![]()
Xác suất để chọn được một học sinh nữ là: 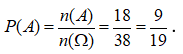
Câu 37:
Một hộp đựng 7 viên bi đỏ đánh số từ 1 đến 7 và 6 viên bi xanh đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
 Xem đáp án
Xem đáp án
Chọn A
Gọi x là số lần viên bi đỏ được chọn.
Gọi y là số lần viên bi xanh được chọn.
TH1. 1x6.
Có 6 cách chọn viên đỏ.
Có 5 cách chọn viên xanh.
=> Có 5.6 = 30 cách.
TH2. x = 7.
Có 6 cách chọn viên xanh.
=> Có 6 cách.
Vậy có 36 cách chọn.
Câu 38:
Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi biến cố A: “5 quả lấy ra có đủ hai màu”. Suy ra biến cố : “5 quả lấy ra chỉ có 1 màu”.
TH1: Lấy ra từ hộp 5 quả cầu xanh, có = 252 cách.
TH2: Lấy ra từ hộp 5 quả cầu đỏ, có = 1 cách.
Suy ra: ![]()
Xác suất để được 5 quả có đủ hai màu là: 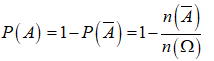

Vậy xác suất cần tìm là
Câu 39:
Một tổ học sinh có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ.
 Xem đáp án
Xem đáp án
Chọn B
Số cách chọn 2 học sinh trong 10 học sinh là .
Nên số phần tử của không gian mẫu là ![]() .
.
Gọi A : “ Biến cố chọn được hai học sinh đều là học sinh nữ”.
Số cách chọn 2 học sinh nữ trong 3 học sinh nữ là .
Khi đó số phần tử của biến cố A là n(A) = = 3.
Vậy xác suất để chọn được hai học sinh đều là nữ là 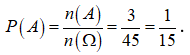
Câu 40:
Lấy ngẫu nhiên một số nguyên dương không vượt quá 10000. Xác suất để số lấy được là bình phương của một số tự nhiên bằng? (tính dưới dạng %)
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử của không gian mẫu: ![]() .
.
Gọi A là biến cố “Số lấy được là bình phương của một số tự nhiên”.
Bình phương của một số tự nhiên có dạng: ![]()
Ta có ![]() .
.
Vậy 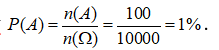 .
.
