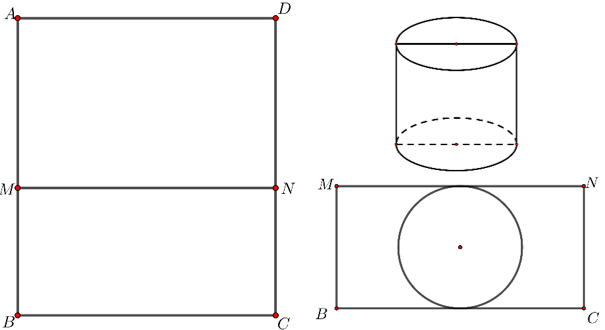
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng $1{\mathrm{m}}^2$ và cạnh BC=x(m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành 2 hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM; phần hình chữ nhật BCNM được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị  để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).

Với x>0, đạo hàm của hàm số $y={\log }_{2}x$ là

Hàm số $y=\frac{x-7}{x+4}$ đồng biến trên khoảng

Cho hàm số y=f(x) là hàm số bậc bốn thỏa mãn f(0)=0. Hàm số y=f'(x) có bảng biến thiên như sau:

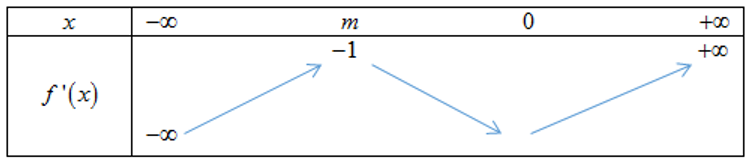
Hàm số $g\left(x\right)=\left|f\left(x^2\right)-x^2\right|$ có bao nhiêu điểm cực trị?

Thể tích của khối hộp chữ nhật có ba kích thước  5; 7; 8 bằng

Với a là số thực dương tùy ý , $\sqrt[4]{a^7}$ bằng

Cho một khối trụ có độ dài đường sinh là l=6cm và bán kính đường tròn đáy là r=5cm. Diện tích toàn phần của khối trụ là

Cho hàm số y=f(x) có bảng biến thiên như sau

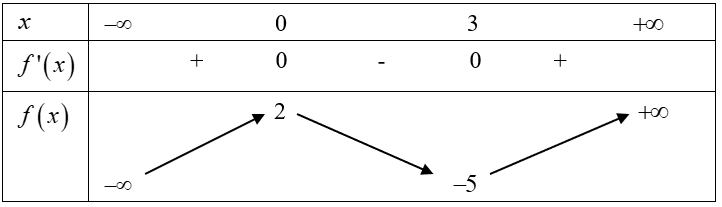
Hàm số f(x) đạt cực đại tại điểm

Với a là số thực dương tùy ý, ${\log }_5\left(\frac{125}{a}\right)$ bằng

Trong không gian Oxyz, mặt cầu tâm là điểm I(2;-3;1) và đi qua điểm M(0;-1;2) có phương trình là:

Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;3;1), B(0;2;1) và mặt phẳng $\left(P\right):x+y+z-7=0.$ Đường thẳng d nằm trong (P) sao cho mọi điểm của d cách đều hai điểm A,B có phương trình làcác mệnh đề sau, mệnh đề nào đúng?

Một khối chóp có thể tích bằng 90 và diện tích đáy bằng 5. Chiều cao của khối chóp đó bằng

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $AB=\sqrt{6}$, $AD=\sqrt{3}$, tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng (SAB), (SAC) tạo với nhau góc $\alpha$ thỏa mãn $\tan \alpha =\frac{3}{4}$ và cạnh SC=3. Thể tích khối S.ABCD bằng:

Nghiệm dương của phương trình $7^{x^2+1}=16807$ là

Cho hàm số y=f(x) xác định và liên tục trên khoảng $\left(-\infty ;+\infty \right),$ có bảng biến thiên như hình sau:

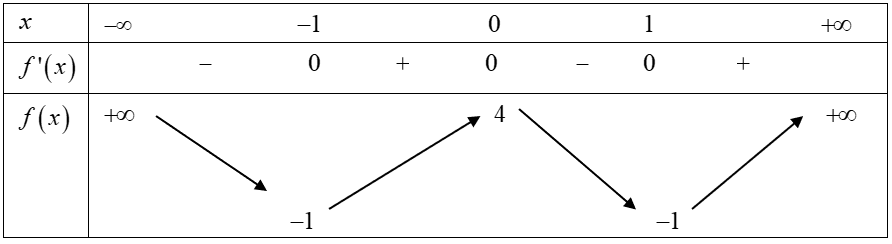
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $AB=AD=2\sqrt{2}$ và $AA\text{'}=4\sqrt{3}$ (tham khảo hình bên). Góc giữa đường thẳng CA' và mặt phẳng (ABCD) bằng