Có tất cả bao nhiêu số phức z mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn và
A. 1
B. 3
C. 2
D. 0
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Gọi điểm M(x;y) là điểm (x;y) trên mp tọa độ biểu diễn số phức
. Khi đó tập hợp điểm M(x;y) biểu diễn số phức z là hai cạnh đối AD,BC của hình vuông ABCD độ dài cạnh bằng và tâm là gốc tọa độ
O.
.Tập hợp điểm M(x;y) biểu diễn số phức là đường tròn tâm .
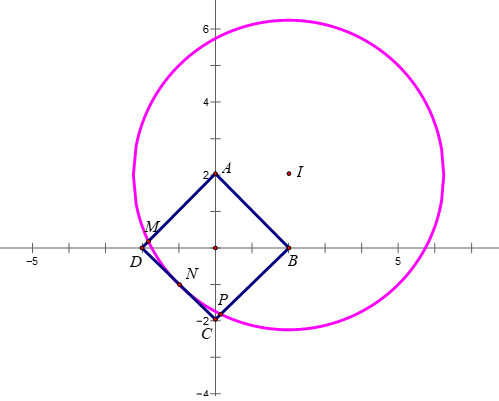
Vậy có 2 điểm biểu diễn M,P thỏa yêu cầu bài toán.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng (ABCD), SA=a. Góc giữa hai mặt phẳng (SCD) và (ABCD) là . Khi đó, nhận giá trị nào trong các giá trị sau ?
Cho hàm số y=f(x) có đạo hàm và f(0)=1. Số điểm cực tiểu của hàm số là
Cho hình chóp tứ giác đều S.ABCD, đáy có tâm là O và . Khi đó, khoảng cách từ điểm O đến mặt phẳng (SAD) bằng bao nhiêu ?
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng 2 và chiều cao bằng một nửa cạnh đáy là
Cho khối hộp có đáy là hình vuông cạnh bằng 5 và chiều cao khối hộp bằng một nửa chu vi đáy. Thể tích của khối hộp đã cho bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có . Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính thể tích V của khối khóp S.ABC.
Một hình trụ có bán kính R=6cm và độ dài đường sinh l=4cm. Tính diện tích toàn phần của hình trụ đó
Cho parabol cắt trục hoành tại hai điểm A, B và đường thẳng d:y=a (0<a<4). Xét parabol đi qua A, B và có đỉnh thuộc đường thẳng y=a. Gọi là diện tích hình phẳng giới hạn bởi và d. là diện tích hình phẳng giới hạn bởi và trục hoành. Biết (tham khảo hình vẽ bên).
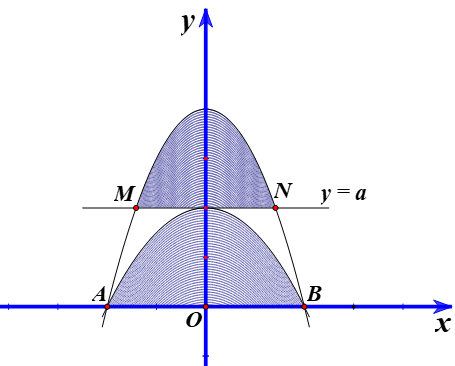
Tính