Mặt phẳng đi qua 3 điểm $M\left(1;0;0\right),N\left(0;-1;0\right),P\left(0;0;2\right)$ có phương trình là

Cho hàm số y=f(x) hàm số y=f'(x) liên tục trên $ℝ$ và có đồ thị như hình vẽ bên. Với giá trị nào của tham số m thì phương trình $f\left(x\right)=3x+m$ có nghiệm thuộc khoảng (-1;1)

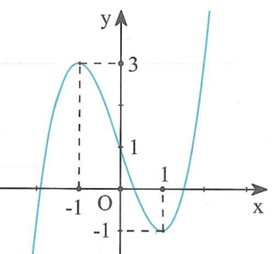
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có $A\left(0;1;-1\right);B\left(1;1;2\right);$ $C\left(1;-1;0\right);D\left(0;0;1\right).$ Tính độ dài đường cao AH của hình chóp A.BCD

Cho hàm số y=f(x) có bảng biến thiên như sau

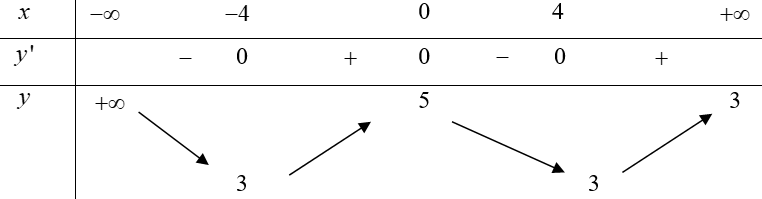
Hàm số g(x)=f(x)+2020 nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y=\frac{x^3}{3}-2x^2+3x+1.$ Giá trị cực tiểu của hàm số đã cho bằng

Cho hàm số $y=x^4-3{\text{x}}^2+m$ có đồ thị $\left(C_m\right)$ với m là tham số thực. giả sử $\left(C_m\right)$ cắt trục Ox tại bốn điểm phân biệt như hình vẽ. Gọi $S_1,S_2$ và $S_3$ là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm m để $S_1+S_2=S_3$

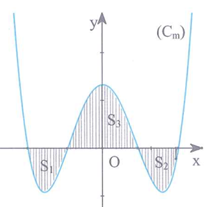
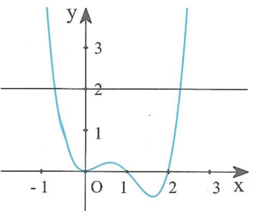
Cho hàm số y=f(x) có đồ thị như hình vẽ bên.

Đồ thị hàm số $y=\frac{f\left(x\right).\sqrt{x^2+x}}{\left[f\left(x\right)-2\right]\left(x^2-1\right)\left(x^2-4\right)\left(2x+1\right)}$ có bao nhiêu đường tiệm cận đứng?

Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy, một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính phía trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bể dày của lớp vỏ thủy tinh).

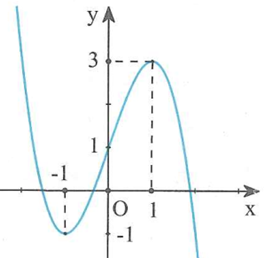
Cho hàm số $f\left(x\right)=a{x}^3+b{x}^2+cx+d\left(a,b,c,d\in ℝ\right).$ Đồ thị của hàm số y=f(x) như hình vẽ bên.

Số nghiệm thực cùa phương trình $3f\left(x\right)+4=0$ là

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm $A\left(7;2;3\right),B\left(1;4;3\right),C(1;2;6),D\left(1;2;3\right)$ và điểm M tùy ý. Tính độ dài đoạn OM khi biểu thức $P=MA+MB+MC+\sqrt{3}MD$ đạt giá trị nhỏ nhất

Cho lăng trụ ABC.A'B'C' trên các cạnh AA', BB', lấy các điểm M, N sao cho $AA\text{'}=4A\text{'}M,BB\text{'}=4B\text{'}N.$ Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi $V_1$ là thể tích của khối chóp $C\text{'}.A\text{'}B\text{'}NM,{V_2}_{}$ là thể tích của khối đa diện ABCMNC'. Tỉ số $\frac{V_1}{V_2}$ bằng

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD là $\frac{a^3}{3}.$ Tính góc $\phi$ giữa đường thẳng SB và mặt phẳng (SCD)

Tính diện tích xung quanh $S_{xq}$ của hình nón có bán kính đáy r=3 và độ dài đường sinh l=5

Cho hàm số y=f(x) có bảng biến thiên như sau

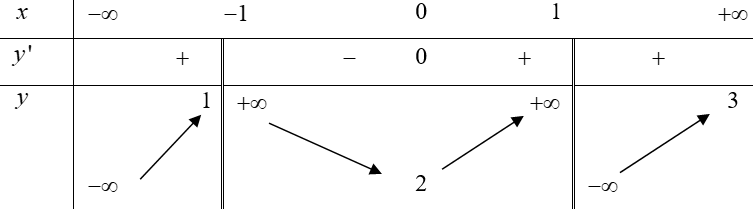
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

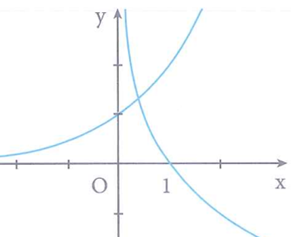
Cho hai hàm số $y=a^x$ và $y={\log }_{b}x$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?

Đường thẳng d: y=x+m cắt đồ thị hàm số $y=\frac{x-1}{x+1}$ tại 2 điểm phân biệt A, B sao cho $O{A}^2+O{B}^2=2,O$ là gốc tọa độ. Khi đó m thuộc khoảng nào dưới đây?