Cho số phức z thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính M+m.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
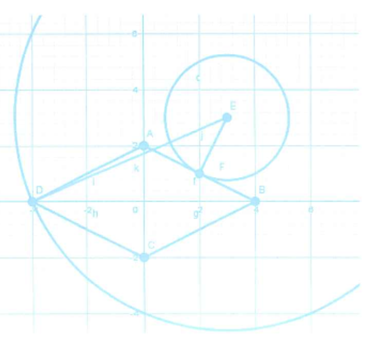
Gọi z=x+yi, , ta có , tập hợp K(x;y) biểu diễn số phức z thuộc các cạnh của hình thoi ABCD như hình vẽ.
đạt giá trị lớn nhất khi KM lớn nhất, theo hình vẽ ta có KM lớn nhất khi hay K(-4;0) suy ra .
đạt giá trị nhỏ nhất khi KM nhỏ nhất, theo hình vẽ ta có KM nhỏ nhất khi (F là hình chiếu của E trên AB).
Suy ra F(2;1) do AE=BE nên F là trung điểm của AB.
Suy ra . Vậy .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau
![]()
Hàm số nghịch biến trên khoảng nào dưới đây?
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt phẳng (ABCD). Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là điểm I với
Cho số phức z thỏa mãn điều kiện với i là đơn vị ảo. Phần ảo của số phức z là
Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của B' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Cạnh bên BB' hợp với đáy (ABC) góc 60°. Khoảng cách từ A đến mặt phẳng (BCC'B') là
Tổng n số hạng đẩu tiên của một cấp số cộng là với . Tìm số hạng đầu tiên và công sai d của cấp số cộng đã cho
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;1;2), B(-3;0;1), C(8;2;-6). Tìm tọa độ trọng tâm G của tam giác ABC
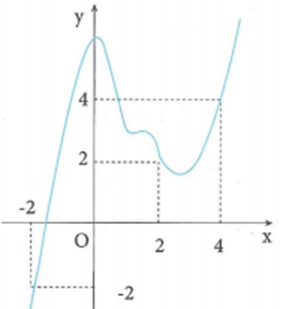
Cho hàm số y=f(x) có đạo hàm liên tục trên . Đồ thị hàm số y=f(x) như hình vẽ bên. Khi đó giá trị của biểu thức bằng bao nhiêu ?
Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là đúng?
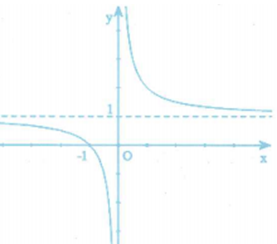
Gọi , lần lượt có điểm biểu diễn là M, N trên mặt phẳng phức (hình bên). Khi đó phần ảo của số phức là
Cho hình lăng trụ đứng , và có AB=a, AC=2a. Gọi I, K lần lượt là trung điểm của các cạnh ; . Tính khoảng cách từ điểm I đến mặt phẳng
Hình bên là đồ thị của ba hàm số , , , được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây đúng

Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai màu