Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-1;1;0), B(0;0;-2), C(1;1;1). Phương trình mặt phẳng (P) nào sau đây thỏa mãn (P) đi qua A, B sao cho khoảng cách từ điểm C đến mặt phẳng (P) bằng $\sqrt{3}$?

Khối lăng trụ ABC.A'B'C' có thể tích V khi đó thể tích khối chóp tứ giác A.BCC'B' bằng

Cho hàm số y = log₂x. Khẳng định nào sau đây sai?

Cho hàm số y = f(x) thỏa mãn $f\text{'}\left(x\right).f\left(x\right)=x^4+x^2$ với mọi số thực x, biết f(0)=2. Tính $f^2\left(2\right)$.

Cho hàm số y = f(x) là hàm đa thức bậc bốn có f(3) < 0, đồ thị hàm số y = f’(x) như hình vẽ.

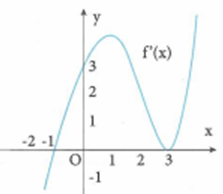
Số điểm cực trị của hàm số $g\left(x\right)={\left[f\left(x-1\right)\right]}^{2020}$ là:

Phương trình $9^{x+1}-{13.6}^x+4^{x+1}=0$ có 2 nghiệm $x_1; x_2$. Phát biểu nào sau đây đúng?

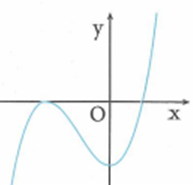
Cho hàm số bậc ba f(x) = ax³ +bx² + cx + d ($a,b,c,d\in ℝ,a\ne 0$ ) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?

Hình chóp có 20 cạnh thì có bao nhiêu mặt?

Cho hàm số f(x) thỏa mãn ${\left(f\text{'}\left(x\right)\right)}^2+f\left(x\right).f"\left(x\right)=x^3-2x,\forall x\in ℝ$ và $f\left(0\right)=f\text{'}\left(0\right)=1$. Tính giá trị của $T=f^2\left(2\right)$

Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S): x² + y² + z² = 8 và điểm $M\left(\frac{1}{2};\frac{\sqrt{3}}{2};0\right)$. Đường thẳng d thay đổi đi qua M và cắt mặt cầu (S) tại hai điểm A, B phân biệt. Tính diện tích S lớn nhất của tam giác OAB.

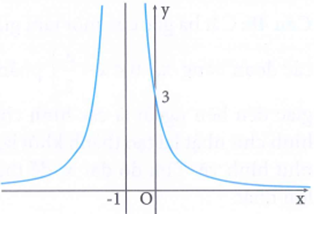
Cho hàm số $f\left(x\right)=\frac{ax+b}{cx+d}$ (với a, b, c, d là các số thực) có đồ thị hàm số f'(x) như hình vẽ. Biết rằng giá trị lớn nhất của hàm số y = f (x) trên đoạn [-3;-2] bằng 7. Giá trị f(2) bằng

Cho hình lăng trụ ABC.A'B'C' có mặt đáy là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng $60°$. Tang góc giữa hai mặt phẳng (BCC'B') và (ABC) bằng

Cho hình chóp S.ABC có SA, AB, AC đôi một vuông góc, AB = a, $AC=a\sqrt{2}$ và diện tích tam giác SBC bằng $\frac{a^2\sqrt{33}}{6}$. Khoảng cách từ điểm A đến măt phẳng (SBC) bằng

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;-2), B(2;1;-1). Tìm tọa độ trọng tâm G của tam giác OAB

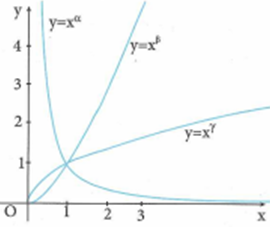
Cho các hàm số lũy thừa $y=x^{\alpha },y=x^{\beta },y=x^{\gamma }$ có đồ thị như hình vẽ. Mệnh để đúng là

Cho hàm số $y=\frac{1}{3}{x}^3+m{x}^2-2x-2m-\frac{1}{3}\left(C\right)$. Tham số $m\in \left(0;\frac{5}{6}\right)$ sao cho diện tích hình phẳng giới hạn bởi đổ thị (C) và các đường x = 0; x = 2; y = 0 bằng 4 có dạng $m_0=\frac{a}{b},\frac{a}{b}$ là phân số tối giản. Khi đó a - b bằng: