Giải thích vì sao các cặp bất phương trình sau tương đương?

a) -4x + 1 > 0 và 4x - 1 < 0

b) 2x² + 5 ≤ 2x - 1 và 2x² - 2x + 6 ≤ 0

$$\begin{gathered} c) x+1>0 và x+1+\frac{1}{x^2+1}>\frac{1}{x^2+1} \\ d)\sqrt{x-1}\ge x và (2x+1)\sqrt{x-1}\ge x(2x+1) \end{gathered}$$

a) Nhân hai vế của BPT: –4x + 1 > 0 với (–1) < 0 ta được BPT: 4x – 1 < 0 nên hai BPT đó tương đương.

Viết là –4x + 1 > 0 ⇔ 4x – 1 < 0.

b) Ta có:

2x² + 5 ≤ 2x – 1

⇔ 2x² + 5 + 1 – 2x ≤ 2x – 1 + 1 – 2x (Cộng cả hai vế của BPT với 1 – 2x).

⇔ 2x² – 2x + 6 ≤ 0.

Vậy hai BPT đã cho tương đương: 2x² + 5 ≤ 2x – 1 ⇔ 2x² – 2x + 6 ≤ 0.

c) Với mọi x ta có: x² ≥ 0 nên x² + 1 > 0 với mọi x. Do đó, 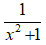 luôn xác định với mọi x.

Ta có: x + 1 > 0

d) Điều kiện x ≥ 1, khi đó 2x + 1 > 0.

Kiến thức áp dụng

Khi sử dụng các phép biến đổi tương đương ta nhận được các BPT tương đương.

Các phép biến đổi tương đương gồm:

+ Cộng hoặc trừ hai vế của BPT với cùng một biểu thức:

     P(x) < Q(x) ⇔ P(x) + f(x) < Q(x) + f(x).

+ Nhân hoặc chia hai vế của BPT với cùng một biểu thức khác 0.

     P (x) < Q(x) ⇔ P(x).f(x) < Q(x).f(x) nếu f(x) > 0

     P(x) < Q(x) ⇔ P(x).f(x) > Q(x).f(x) nếu f(x) < 0.

+ Nâng lên lũy thừa bậc chẵn của BPT có cả hai vế đều dương:

     0 < P(x) < Q(x) ⇔ P²ⁿ(x) < Q²ⁿ(x)

+ Nâng lên lũy thừa bậc lẻ cả hai vế của BPT

     P(x) < Q(x) ⇔ P²ⁿ⁺¹(x) < Q²ⁿ⁺¹(x).

+ Khai căn bậc hai của BPT có cả hai vế đều dương :

     0 < P(x) < Q(x) ⇔ √P(x) < √Q(x)

+ Khai căn bậc ba cả hai vế của BPT :