Tính hệ số góc của đường thẳng d có vectơ chỉ phương là u→ = (-1; √3).

Cho tam giác ABC biết A(1; 4), B(3; -1) và C(6; 2).

a, Lập phương trình tổng quát của các đường thẳng AB, BC và CA.

b, Lập phương trình tổng quát của đường cao AH và trung tuyến AM.

Hãy tìm tọa độ của vectơ chỉ phương của đường thẳng có phương trình: 3x + 4y + 5 = 0.

Xét vị trí tương đối của các cặp đường thẳng d₁ và d₂ sau đây:

Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:

a, A(3; 5) và Δ : 4x + 3y +1 = 0

b, B(1; -2) và d: 3x – 4y -26 = 0

c, C(1; 2) và m: 3x + 4y -11 = 0

Tìm bán kính của đường tròn tâm C(-2; -2) tiếp xúc với đường thẳng Δ : 5x + 12y -10 = 0.

Cho đường thẳng d có phương trình tham số:

Tìm điểm M thuộc đường thẳng d và cách điểm A(0 ; 1) một khoảng bằng 5.

Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d₁: 4x – 2y + 6 = 0 và d₂: x – 3y + 1 = 0

Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:

d₁: -3x + 6y – 3 = 0;

d₂: y = -2x;

d₃: 2x + 5 = 4y.

Viết phương trình tổng quát của đường thẳng đi qua điểm M(4; 0) và điểm N(0; -1).

Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:

a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương  ;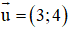

b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến .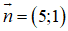

Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây:

d₁: x – 2y = 0;

d₂: x = 2;

d₃: y + 1 = 0;

d₄: x/8 + y/4 = 1.

Hãy tìm một điểm có tọa độ xác định và một vectơ chỉ phương của đường thẳng có phương trình tham số

Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y = $\frac{1}{2x}$

a) Tìm tung độ của hai điểm M_o và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.

b) Cho vectơ u→ = (2; 1). Hãy chứng tỏ 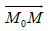 cùng phương với u.

Tính khoảng cách từ các điểm M(-2; 1) và O(0; 0) đến đường thẳng Δ có phương trình 3x – 2y - 1 = 0.

Lập phương trình tổng quát của đường thẳng Δ trong mỗi trường hợp sau:

a) Δ đi qua M(–5; –8) và có hệ số góc k = –3;

b) Δ đi qua hai điểm A(2; 1) và B(–4; 5).