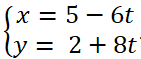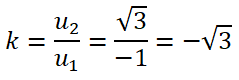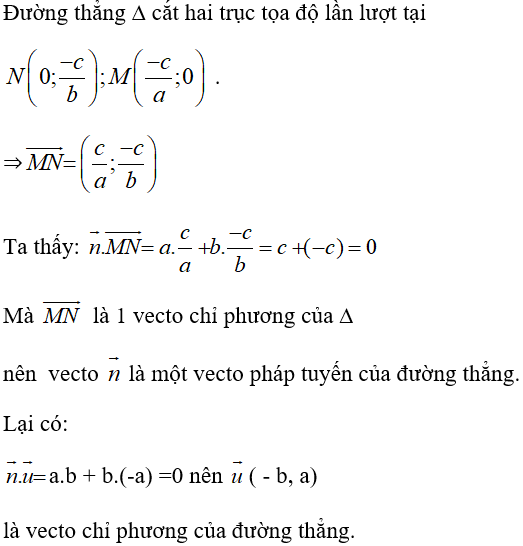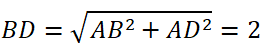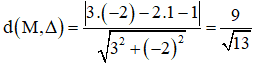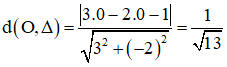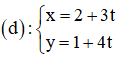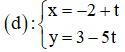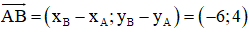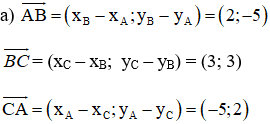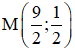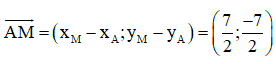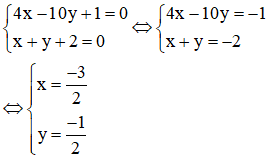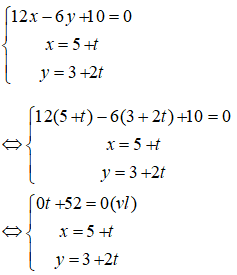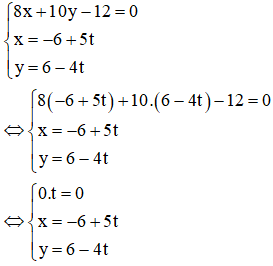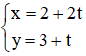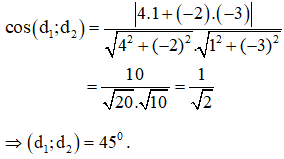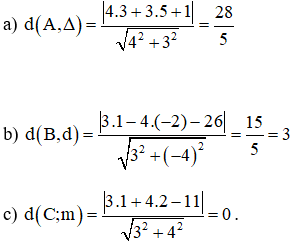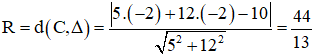Bài 1: Phương trình đường thẳng
-
2216 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y =
a) Tìm tung độ của hai điểm Mo và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.
b) Cho vectơ u→ = (2; 1). Hãy chứng tỏ 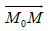
 Xem đáp án
Xem đáp án
a) Với x = 2 ⇒ y = 1/2 x = 1/2 .2 = 1 ⇒ Mo (2;1)
x = 6 ⇒ y = 1/2 x = 1/2 .6 = 3 ⇒ M (6;3)
b) 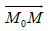
Vậy 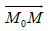
Câu 2:
Hãy tìm một điểm có tọa độ xác định và một vectơ chỉ phương của đường thẳng có phương trình tham số
 Xem đáp án
Xem đáp án
Một điểm thuộc đường thẳng là (5; 2)
Một vecto chỉ phương là u→ (-6;8)
Câu 3:
Tính hệ số góc của đường thẳng d có vectơ chỉ phương là u→ = (-1; √3).
 Xem đáp án
Xem đáp án
Hệ số góc của đường thẳng d có vectơ chỉ phương u→ = (-1; √3) là:
Câu 5:
Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 74: Hãy chứng minh nhận xét trên.
 Xem đáp án
Xem đáp án
Chọn N(0; -c/b); M(-c/a;0) thuộc đường thẳng Δ.
⇒MN→ =(c/a; (-c)/b)
Ta thấy n→.MN→ = 0
Vậy n→ = (a;b) là vecto pháp tuyến của đường thẳng.
n→.u→ = a.b - b.a = 0 nên u→ (-b;a) là vecto chỉ phương của đường thẳng.
Câu 6:
Hãy tìm tọa độ của vectơ chỉ phương của đường thẳng có phương trình: 3x + 4y + 5 = 0.
 Xem đáp án
Xem đáp án
Vecto pháp tuyến của đường thẳng làn→ = (3;4)
⇒ Vecto chỉ phương của đường thẳng là u→ (-4;3).
Câu 7:
Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây:
d1: x – 2y = 0;
d2: x = 2;
d3: y + 1 = 0;
d4: x/8 + y/4 = 1.
 Xem đáp án
Xem đáp án
+) Đường thẳng d1: x – 2y = 0 đi qua gốc tọa độ O và điểm (2; 1).
+) đường thẳng d2: x = 2 là đường thẳng đi qua điểm (2; 0) và song song với trục Oy.
+) Đường thẳng d3: y +1 = 0 là đường thẳng đi qua điểm (0; -1) và song song với trục Ox.
+) Đường thẳng d4: 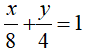
Câu 8:
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
 Xem đáp án
Xem đáp án
Xét Δ và d1, hệ phương trình: 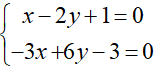
Xét Δ và d2, hệ phương trình: 
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 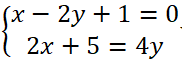
Vậy Δ // d3
Câu 9:
Cho hình chữ nhật ABCD có tâm I và cạnh AB = 1, AD = √3. Tính số đo các góc ∠(AID) và ∠(DIC) .
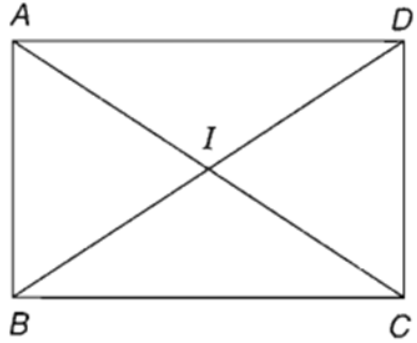
 Xem đáp án
Xem đáp án
Xét ΔABD vuông tại A có:
Do ABCD là hình chữ nhật tâm I nên:
AI = IC = ID = 1/2 BD = 1
ΔICD có ID = IC = DC = 1
⇒ΔICD đều ⇒ ∠(DIC) = 60o
Ta có: ∠(DIC) + ∠(AID ) = 180o⇒ ∠(AID ) = 180o- 60o= 120o
Câu 10:
Tính khoảng cách từ các điểm M(-2; 1) và O(0; 0) đến đường thẳng Δ có phương trình 3x – 2y - 1 = 0.
 Xem đáp án
Xem đáp án
Khoảng cách từ điểm M (-2; 1) đến đường thẳng Δ là:
Khoảng cách từ điểm O (0; 0) đến đường thẳng Δ là:
Câu 11:
Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:
a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương 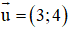
b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến 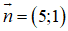
 Xem đáp án
Xem đáp án
a) Phương trình tham số của d là:
b) d nhận 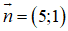
⇒ d nhận 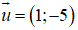
Phương trình tham số của đường thẳng d là:
Câu 12:
Lập phương trình tổng quát của đường thẳng Δ trong mỗi trường hợp sau:
a) Δ đi qua M(–5; –8) và có hệ số góc k = –3;
b) Δ đi qua hai điểm A(2; 1) và B(–4; 5).
 Xem đáp án
Xem đáp án
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận 
⇒ Δ nhận 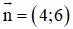
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.
Câu 13:
Cho tam giác ABC biết A(1; 4), B(3; -1) và C(6; 2).
a, Lập phương trình tổng quát của các đường thẳng AB, BC và CA.
b, Lập phương trình tổng quát của đường cao AH và trung tuyến AM.
 Xem đáp án
Xem đáp án
+ Lập phương trình đường thẳng AB:
Đường thẳng AB nhận 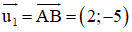
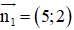
Mà A(1; 4) thuộc AB
⇒ PT đường thẳng AB: 5(x- 1) + 2(y – 4) = 0 hay 5x + 2y – 13 = 0.
+ Lập phương trình đường thẳng BC:
Đường thẳng BC nhận 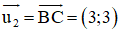
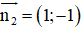
Mà B(3; –1) thuộc BC
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y + 1) = 0 hay x – y – 4 = 0.
+ Lập phương trình đường thẳng CA:
Đường thẳng CA nhận 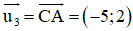
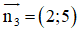
Mà C(6; 2) thuộc CA
⇒ Phương trình đường thẳng AC: 2(x – 6) + 5(y - 2) = 0 hay 2x + 5y – 22 = 0.
b) + AH là đường cao của tam giác ABC ⇒ AH ⊥ BC
⇒ Đường thẳng AH nhận 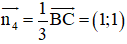
Mà A(1; 4) thuộc AH
⇒ Phương trình đường thẳng AH: 1(x - 1) + 1(y - 4) = 0 hay x + y – 5 = 0.
+ Trung điểm M của BC có tọa độ 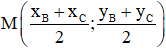
Đường thẳng AM nhận 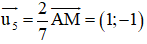
⇒ AM nhận 
Mà A(1; 4) thuộc AM
⇒ Phương trình đường thẳng AM: 1(x - 1) + 1(y – 4) = 0 hay x + y – 5 = 0.
Câu 14:
Viết phương trình tổng quát của đường thẳng đi qua điểm M(4; 0) và điểm N(0; -1).
 Xem đáp án
Xem đáp án
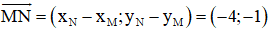
Đường thẳng MN nhận 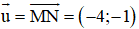
⇒ MN nhận 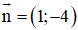
Mà M(4; 0) thuộc đường thẳng MN
⇒ Phương trình đường thẳng MN: 1(x - 4) – 4(y - 0) = 0 hay x – 4y – 4 = 0
Câu 15:
Xét vị trí tương đối của các cặp đường thẳng d1 và d2 sau đây:
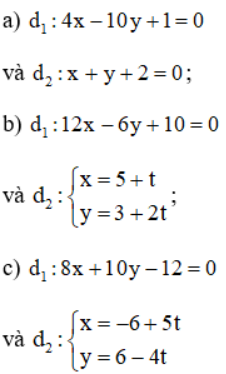
 Xem đáp án
Xem đáp án
Cách 1: Dựa vào số nghiệm của hệ phương trình:
a) Xét hệ phương trình
Hệ phương trình có nghiệm duy nhất nên (d1) cắt (d2).
b) Xét hệ phương trình
Hệ phương trình trên vô nghiệm nên hai đường thẳng trên song song.
c) Xét hệ phương trình
Hệ phương trình trên có vô số nghiệm nên hai đường thẳng trùng nhau.
Cách 2: Dựa vào vị trí tương đối của các vectơ chỉ phương (hoặc vectơ pháp tuyến).
a) d1 nhận 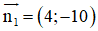
d2 nhận 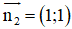
Nhận thấy 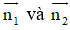
b) d1 nhận 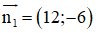
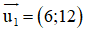
d2 nhận 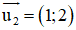
Nhận thấy 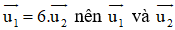
⇒ d1 và d2 song song hoặc trùng nhau.
Xét điểm M(5;3) có:
M(5; 3) ∈ d2
12.5 – 6.3 + 10 = 52 ≠ 0 nên M(5; 3) ∉ d1.
Vậy d1 và d2 song song.
c) d1 nhận 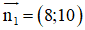
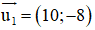
d2 nhận 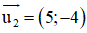
Nhận thấy 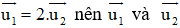
⇒ d1 và d2 song song hoặc trùng nhau.
Xét M(–6; 6) ∈ d2; M(–6; 6) ∈ d1 (Vì 8.(–6) + 10.6 – 12 = 0)
⇒ d1 và d2 trùng nhau.
Câu 16:
Cho đường thẳng d có phương trình tham số:
Tìm điểm M thuộc đường thẳng d và cách điểm A(0 ; 1) một khoảng bằng 5.
 Xem đáp án
Xem đáp án
M ∈ d nên M có tọa độ: M(2 + 2t; 3 + t).
Khi đó : AM2 = (xM – xA)2 + (yM – yA)2 = (2+2t)2 + (2 + t)2 = 5t2 + 12t + 8.
Ta có : AM = 5 ⇔ AM2 = 25
⇔ 5t2 + 12t + 8 = 25
⇔ 5t2 + 12t – 17 = 0
⇔ t = 1 hoặc t = –17/5.
+ Với t = 1 thì M(4 ; 4).
+ Với t = –17/5 thì M(–24/5 ; –2/5).
Vậy có hai điểm M thỏa mãn là M(4 ; 4) và M(–24/5 ; –2/5).
Câu 17:
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
 Xem đáp án
Xem đáp án
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
Câu 19:
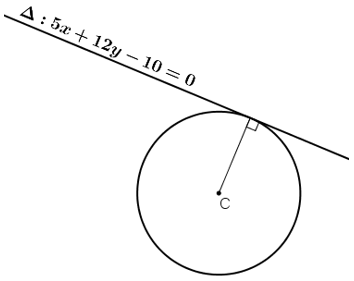
Tìm bán kính của đường tròn tâm C(-2; -2) tiếp xúc với đường thẳng Δ : 5x + 12y -10 = 0.
 Xem đáp án
Xem đáp án
Vì đường tròn tâm C tiếp xúc với Δ nên R = d(C, Δ).
Do đó ta có :