Cho hàm số y=f(x)có đạo hàm f′(x)=x2(x2−1). Điểm cực tiểu của hàm số y=f(x) là:
 Giải bởi Vietjack
Giải bởi Vietjack
Bước 1: Giải phương trìnhf′(x)=0
Ta có:
f′(x)=0⇔[x=0(nghiemboichan)x2−1=0⇔[x=1(nghiemboile)x=−1(nghiemboile)
Bước 2: Lập BBT của hàm số từ đó xác định điểm cực tiểu của hàm số.
BBT:
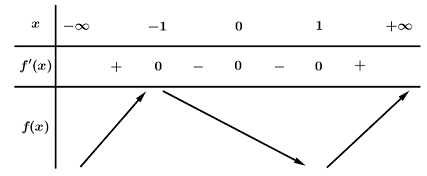
Vậy điểm cực tiểu của hàm số là x=1.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điều kiện để hàm số bậc ba không có cực trị là phương trình y′=0 có:
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
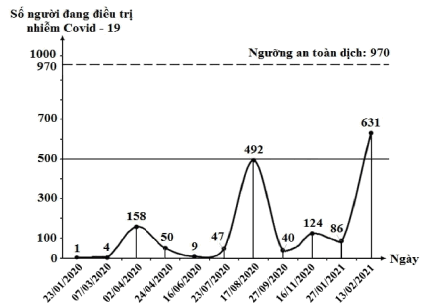
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
Cho các phát biểu sau:
1. Hàm số y=f(x) đạt cực đại tại x0 khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua x0.
2. Hàm số y=f(x) đạt cực trị tại x0 khi và chỉ khi x0 là nghiệm của đạo hàm.
3. Nếu f′(x0)=0 và f′′(x0)=0 thì x0 không phải là cực trị của hàm số y=f(x) đã cho.
4. Nếu f′(x0)=0 và f′′(xo)>0 thì hàm số đạt cực đại tại x0.
Các phát biểu đúng là:
Cho hàm số f(x)=ax3+bx2+cx+d (với a,b,c,d∈R và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g(x)=f(−2x2+4x) là
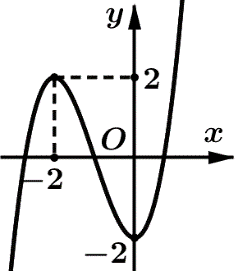
Cho hàm số y=f(x) có bảng biến thiên như sau:
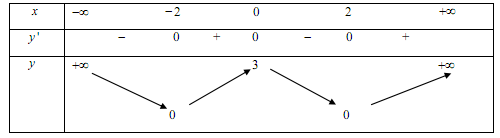
Khẳng định nào sau đây là khẳng định sai:
Cho hàm số f(x) có đạo hàm f′(x)=x(x−1)(x+4)3,∀x∈R. Số điểm cực tiểu của hàm số đã cho là:
Cho hàm số f(x) có đạo hàm f′(x)=x2(x+2)(x−3). Điểm cực đại của hàm số g(x)=f(x2−2x) là:
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y=x3−3x2+1 là:
Cho hàm số y=f(x) có đạo hàm trên (a;b). Nếu f′(x) đổi dấu từ âm sang dương qua điểm x0 thuộc (a;b) thì
Giả sử y=f(x) có đạo hàm cấp hai trên (a;b). Nếu {f′(x0)=0f″ thì