Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
A.\[\left( {0; + \infty } \right)\]
B. \[\left[ {0;2} \right]\]
C. \[\left[ {2; + \infty } \right)\]
D. \[\left[ {2; + \infty } \right) \cup \left\{ 0 \right\}\]
Giải bởi Vietjack
ĐK:\[x \ge 0\]
\[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x \Leftrightarrow {3^{\sqrt {2x} + 1}} + 2x \le {3^{x + 1}} + {x^2} \Leftrightarrow {3^{\sqrt {2x} + 1}} + {\left( {\sqrt {2x} } \right)^2} \le {3^{x + 1}} + {x^2}\]
Xét hàm số \[f\left( t \right) = {3^{t + 1}} + {t^2}\]có\[f'\left( t \right) = {3^{t + 1}}.\ln 3 + 2t > 0\,\,\forall t \ge 0 \Rightarrow \] Hàm số đồng biến trên \[\left[ {0; + \infty } \right)\]
Mà\[f\left( {\sqrt {2x} } \right) \le f\left( x \right) \Leftrightarrow \sqrt {2x} \le x \Leftrightarrow 2x \le {x^2} \Leftrightarrow {x^2} - 2x \ge 0 \Leftrightarrow x \in \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right)\]
Mà\[x \ge 0 \Rightarrow x \in \left[ {2; + \infty } \right) \cup \left\{ 0 \right\}\]
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
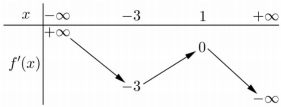
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
Nghiệm của bất phương trình \[{e^x} + {e^{ - x}} < \frac{5}{2}\] là
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
Tìm tập nghiệm của bất phương trình \[{\left( {\frac{1}{2}} \right)^x} \ge 2\].
Tập hợp nghiệm của bất phương trình: \[{3^{3x - 2}} + \frac{1}{{{{27}^x}}} \le \frac{2}{3}\] là:
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
Tập nghiệm của bất phương trình \[{\left( {{x^2} + x + 1} \right)^x} < 1\] là:
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\]
Cho hàm số \[f\left( x \right) = \frac{{{3^x}}}{{{7^{{x^2} - 4}}}}\]. Hỏi khẳng định nào sau đây là sai?
Tìm tập nghiệm S của bất phương trình \[{2^{x - 1}} > {\left( {\frac{1}{{16}}} \right)^{\frac{1}{x}}}\]
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
