Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
A.65021
B.65024
C.65022
D.65023
Giải bởi Vietjack
\[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]
TH1: \(\left\{ {\begin{array}{*{20}{c}}{{3^{{x^2} - x}} - 9 \le 0\,\,\,\,\left( 1 \right)}\\{{2^{{x^2}}} - m \ge 0\,\,\,\,\left( 2 \right)}\end{array}} \right.\,\,\,\,\,\left( I \right)\)
\[\left( 1 \right) \Leftrightarrow {3^{{x^2} - x}} \le {3^2} \Leftrightarrow {x^2} - x \le 2 \Leftrightarrow - 1 \le x \le 2\]
⇒ Số nghiệm nguyên của bất phương trình (1) là 4 nghiệm, gồm \[\left\{ { - 1;0;1;2} \right\}\]
Như vậy hệ có tối đa 4 nghiệm nguyên, hay bất phương trình ban đầu cũng chỉ có tối đa 4 nghiệm nguyên (Loại).
TH2: \(\left\{ {\begin{array}{*{20}{c}}{{3^{{x^2} - x}} - 9 \ge 0\,\,\,\,\left( {1'} \right)}\\{{2^{{x^2}}} - m \le 0\,\,\,\,\left( {2'} \right)}\end{array}} \right.\,\,\,\,\,\left( {II} \right)\)
\[(1\prime ) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \ge 2}\\{x \le - 1}\end{array}} \right.\]
\[\left( {2'} \right) \Leftrightarrow {2^{{x^2}}} \le m \Leftrightarrow {x^2} \le {\log _2}m \Leftrightarrow - \sqrt {{{\log }_2}m} \le x \le \sqrt {{{\log }_2}m} \]
Để (II) có nghiệm thì\(\left\{ {\begin{array}{*{20}{c}}{ - \sqrt {lo{g_2}m} \le - 1}\\{\sqrt {lo{g_2}m} \ge 2}\end{array}} \right.\)
Mà bất phương trình ban đầu có 5 nghiệm nguyên nên các nghiệm đó bắt buộc phải là -3, -2, -1, 2, 3.
Do đó
\[3 \le \sqrt {{{\log }_2}m} < 4 \Leftrightarrow 9 \le {\log _2}m < 16 \Leftrightarrow 512 \le m < 65536\]
Vậy có\[65535 - 512 + 1 = 65024\]giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
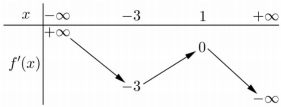
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
Nghiệm của bất phương trình \[{e^x} + {e^{ - x}} < \frac{5}{2}\] là
Tìm tập nghiệm của bất phương trình \[{\left( {\frac{1}{2}} \right)^x} \ge 2\].
Tập hợp nghiệm của bất phương trình: \[{3^{3x - 2}} + \frac{1}{{{{27}^x}}} \le \frac{2}{3}\] là:
Tập nghiệm của bất phương trình \[{\left( {{x^2} + x + 1} \right)^x} < 1\] là:
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
Cho hàm số \[f\left( x \right) = \frac{{{3^x}}}{{{7^{{x^2} - 4}}}}\]. Hỏi khẳng định nào sau đây là sai?
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\]
Tìm tập nghiệm S của bất phương trình \[{2^{x - 1}} > {\left( {\frac{1}{{16}}} \right)^{\frac{1}{x}}}\]
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
