Biểu diễn hình học tập nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau:
 Giải bởi Vietjack
Giải bởi Vietjack
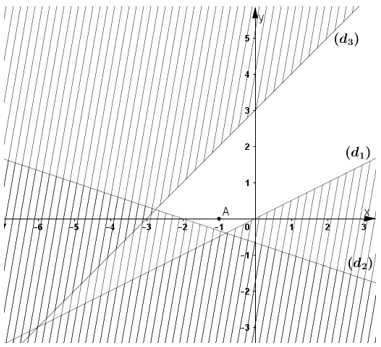
Ta vẽ các đường thẳng x – 2y = 0 (d1) ; x + 3y = –2 (d2) ;
–x + y = 3 (d3).
Điểm A(–1; 0) có tọa độ thỏa mãn tất cả các bất phương
trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (d1);
(d2); (d3) không chứa điểm A.
Miền không bị gạch chéo trong hình vẽ, không tính các
đường thẳng là miền nghiệm của hệ bất phương trình đã cho.
Ta vẽ các đường thẳng 2x + 3y = 6 (d1); 2x – 3y = 3 (d2);
x = 0 (trục tung).
Điểm B(1; 0) có tọa độ thỏa mãn tất cả các bất phương
trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (d1);
(d2) và trục tung không chứa điểm B.
Miền không bị gạch chéo (tam giác MNP, kể cả cạnh MP
và NP, không kể cạnh MN) là miền nghiệm của hệ bất
phương trình đã cho.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau:
a) -x + 2 + 2(y - 2) < 2(1 - x)
b) 3(x - 1) + 4(y - 2) < 5x - 3
Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn: -3x + 2y > 0.
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho trong bảng sau:
| Nhóm | Số máy trong mỗi nhóm | Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm | |
| Loại I | Loại II | ||
| A | 10 | 2 | 2 |
| B | 4 | 0 | 2 |
| C | 12 | 2 | 4 |
Hướng dẫn: Áp dụng phương pháp giải trong mục IV.Một đơn vị sản phẩm I lãi 3 nghìn đồng, một đơn vị sản xuất II lãi 5 nghìn đồng. Hãy lập kế hoạch sản xuất để cho tổng số tiền lãi cao nhất.
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn