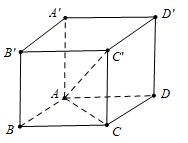
Cho lăng trụ đứng \[ABCD.A'B'C'D'\] có đáy ABCDlà hình chữ nhật với \[AB = 2a,{\rm{ }}AC = 2a\sqrt 3 .\] Góc giữa đường thẳng \[AC'\] và mặt phẳng \[\left( {ABCD} \right)\] bằng \[30^\circ .\] Thể tích của khối lăng trụ \[ABCD.A'B'C'D'\] bằng
A.\[\frac{{16{a^3}}}{3}.\]
B.\[\frac{{8{a^3}\sqrt 2 }}{3}.\]
C.\[8{a^3}\sqrt 2 .\]
D.\[6{a^3}\sqrt 3 .\]
Giải bởi Vietjack
Lời giải:
Chọn đáp án C
Ta có \(\widehat {\left( {AC';(ACBC{\rm{D}})} \right)} = \widehat {C'AC} = 30^\circ \)
\( \Rightarrow \tan 30^\circ = \frac{{CC'}}{{AC}} = \frac{1}{{\sqrt 3 }} \Rightarrow CC' = \frac{{AC}}{{\sqrt 3 }} = 2{\rm{a}}\).
Cạnh \(BC = \sqrt {A{C^2} - A{B^2}} = 2{\rm{a}}\sqrt 2 \Rightarrow V = CC'.AB.BC = 8{{\rm{a}}^3}\sqrt 2 \).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho hai vectơ \[\vec u = \left( {1;0;2} \right)\] và \[\vec v = \left( { - 1;2;0} \right).\] Tính \[P = \cos \left( {\vec u;\vec v} \right).\]
Cho hàm số \[y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1\] (m là tham số thực) có hai điểm cực trị \[{x_1},{\rm{ }}{x_2}\] thỏa mãn \[x_1^2 + x_2^2 = 2.\] Mệnh đề nào dưới đây là đúng?
Cho \[a,{\rm{ }}b,{\rm{ }}x\] là các số thực dương tùy ý thỏa mãn \[{\log _2}x = 2{\log _2}a + 3{\log _2}b.\] Mệnh đề nào dưới đây là đúng?
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \left| {{x^4} - 4{x^3} - 8{x^2} - m} \right|\] có đúng 7 điểm cực trị?
Tính đạo hàm của hàm số \[y = {\log _{\frac{2}{3}}}\sqrt {{x^2} + 1} .\]
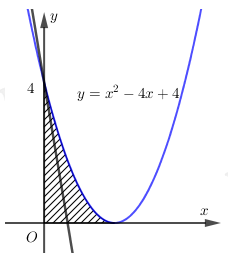
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y = {x^2} - 4x + 4\], trục tung và trục hoành. Xác định \[k\] để đường thẳng d đi qua điểm \[A\left( {0;4} \right)\] có hệ số góc \[k\] chia (H) thành hai phần có diện tích bằng nhau (như hình vẽ bên).
Cho hàm số f(x) có bảng biến thiên như sau:
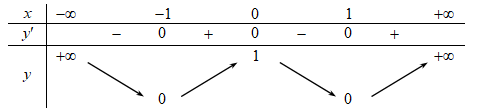
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
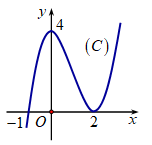
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
Biết rằng \[\int\limits_1^2 {x{{\left( {x - 1} \right)}^n}dx} = \frac{{27}}{{182}},\] với \[n \in {\mathbb{N}^*}.\] Mệnh đề nào dưới đây là đúng?
Giá trị lớn nhất của hàm số \[y = \frac{{{x^2} + 3}}{{x - 1}}\] trên đoạn \[\left[ { - 2;0} \right]\] bằng
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} - {z_2}\] có phần ảo bằng
Cho hàm số f(x) có bảng biến thiên như sau:
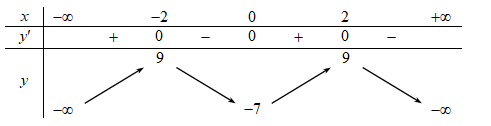
Giá trị cực đại của hàm số đã cho là
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):x - 2y + 3z - 4 = 0.\] Xét mặt phẳng \[\left( Q \right):4x + \left( {m - 1} \right)y + \left( {8 - m} \right)z - 3 = 0,\] với m là tham số thực. Tìm tất cả các giá trị thực của m để mặt phẳng (Q) vuông góc với mặt phẳng (P).
