Trong không gian, cho hình trụ (T) có chiều cao bằng 8cm. Mặt phẳng (α) song song với trục của (T), cắt (T) theo thiết diện (D) là một hình vuông. Khoảng cách từ trục của (T) đến mặt phẳng chứa (D) bằng 3cm. Tính thể tích của khối trụ đã cho.
A.\[210\pi c{m^3}.\]
B.\[200\pi c{m^3}.\]
C.\[280\pi c{m^3}.\]
D.\[270\pi c{m^3}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Chọn đáp án B
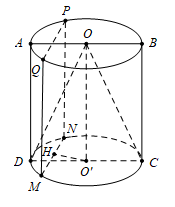
Thiết diện là hình vuông MNPQnhư hình vẽ.
Kẻ \(OH \bot MN \Rightarrow O'H = 3cm\).
Cạnh \(QM = MN = 8cm \Rightarrow HN = 4cm\)
\( \Rightarrow O'N = \sqrt {H{N^2} + O'{H^2}} = \sqrt {{4^2} + {3^2}} = 5cm\)
\( \Rightarrow V = \pi {r^2}h = \pi O'{N^2}.QM = \pi {.5^2}.8 = 200c{m^3}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho hai vectơ \[\vec u = \left( {1;0;2} \right)\] và \[\vec v = \left( { - 1;2;0} \right).\] Tính \[P = \cos \left( {\vec u;\vec v} \right).\]
Cho hàm số \[y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1\] (m là tham số thực) có hai điểm cực trị \[{x_1},{\rm{ }}{x_2}\] thỏa mãn \[x_1^2 + x_2^2 = 2.\] Mệnh đề nào dưới đây là đúng?
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \left| {{x^4} - 4{x^3} - 8{x^2} - m} \right|\] có đúng 7 điểm cực trị?
Cho \[a,{\rm{ }}b,{\rm{ }}x\] là các số thực dương tùy ý thỏa mãn \[{\log _2}x = 2{\log _2}a + 3{\log _2}b.\] Mệnh đề nào dưới đây là đúng?
Tính đạo hàm của hàm số \[y = {\log _{\frac{2}{3}}}\sqrt {{x^2} + 1} .\]
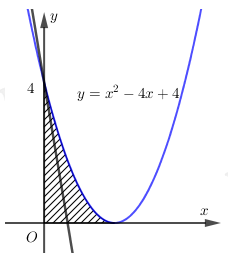
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y = {x^2} - 4x + 4\], trục tung và trục hoành. Xác định \[k\] để đường thẳng d đi qua điểm \[A\left( {0;4} \right)\] có hệ số góc \[k\] chia (H) thành hai phần có diện tích bằng nhau (như hình vẽ bên).
Cho hàm số f(x) có bảng biến thiên như sau:
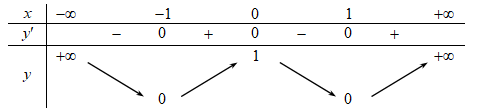
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
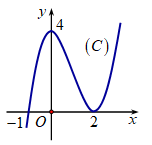
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
Giá trị lớn nhất của hàm số \[y = \frac{{{x^2} + 3}}{{x - 1}}\] trên đoạn \[\left[ { - 2;0} \right]\] bằng
Biết rằng \[\int\limits_1^2 {x{{\left( {x - 1} \right)}^n}dx} = \frac{{27}}{{182}},\] với \[n \in {\mathbb{N}^*}.\] Mệnh đề nào dưới đây là đúng?
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} - {z_2}\] có phần ảo bằng
Cho hàm số f(x) có bảng biến thiên như sau:
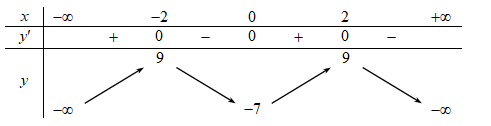
Giá trị cực đại của hàm số đã cho là
Cho khối nón (N) có bán kính đáy bằng 3 và thể tích bằng \[12\pi .\] Tính diện tích xung quanh \[{S_{xq}}\] của (N).