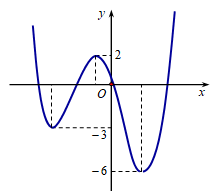
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
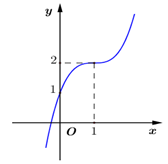
A.\[y = {x^3} - 3{x^2} + 3x + 1.\]
B.\[y = - {x^3} + 3{x^2} + 1.\]
C.\[y = {x^3} - 3x + 4.\]
D.\[y = - {x^3} - 3{x^2} - 1.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A
Ta có \(y\left( 1 \right) = 2 \Rightarrow \) Loại B và D. Mà \(y\left( 0 \right) = 1 \Rightarrow \) Chọn A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho đường thẳng \[d:\frac{{x - 2}}{2} = \frac{{y + 3}}{1} = \frac{{z - 1}}{{ - 2}}.\] Vectơ nào dưới đây là một vectơ chỉ phương của d?
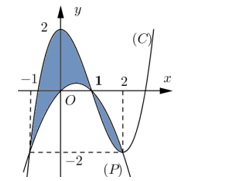
Hình phẳng \[\left( H \right)\] được giới hạn bởi đồ thị (C) của hàm số đa thức bậc ba và parabol \[\left( P \right)\] có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
Cho phương trình phức \[{z^2} - bz + c = 0\] (\[b,{\rm{ }}c \in \mathbb{R}\]) có một nghiệm \[z = 3 + i.\] Tính \[b + c.\]
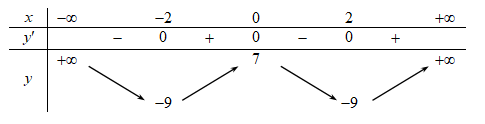
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn \[\left| {z - 1 + 4i} \right| = 2.\]
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 5y - z = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{{ - 1}}.\] Viết phương trình đường thẳng Δ vuông góc mặt phẳng (P) tại giao điểm của đường thẳng dvà mặt phẳng (P).
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
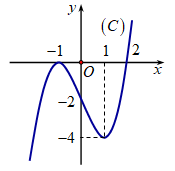
Tính đạo hàm của hàm số \[y = \ln \left( {1 + \sqrt {2x + 1} } \right).\]
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 6y + 12 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Tích phân \[\int\limits_0^{\frac{\pi }{{12}}} {\sin 3xdx} \] bằng
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số \[y = \left| {f\left( {x - 2020} \right) + m} \right|\] có đúng 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
Giải phương trình \[{\log _2}\left( {x + 12} \right).{\log _x}2 = 2.\]
Cho hình thang \[ABCD\] có \[\widehat {BAD} = \widehat {ADC} = 90^\circ \] và \[AB = 8,{\rm{ }}CD = BC = 5.\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình thang \[ABCD\] xung quanh trục \[AB.\]
Tính \[P = \frac{1}{{{{\log }_2}2020!}} + \frac{1}{{{{\log }_3}2020!}} + \frac{1}{{{{\log }_4}2020!}} + .... + \frac{1}{{{{\log }_{2020}}2020!}}.\]